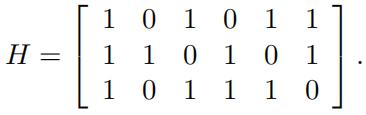School of Mathematics and Statistics
MT4516 Finite Mathematics
Mathematics代写 Consider a code C ⊆ Z n 2 with minimum distance at least 2k + 1. For w ∈ C, let B(w, k) be the Hamming ball with centre w and radius k.
1.The set Zn 2with the Hamming distance d is a metric space. In other words, d has the following properties: Mathematics代写
(i) d(x, y) ≥ 0;
(ii) d(x, y) = 0 ⇐⇒ x = y;
(iii) d(x, y) = d(y, x);
(iv) d(x, z) ≤ d(x, y) + d(y, z) (the triangle inequality); Mathematics代写
for all x, y, z ∈ Zn 2
2.Consider a code C ⊆ Z n 2 with minimum distance at least 2k + 1. For w ∈ C, let B(w, k) be the Hamming ball with centre w and radius k.
Prove that, for distinct w1, w2 ∈ C, we have
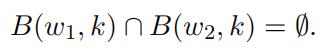
3.Prove that for any x, y ∈ Z n 2we have
wt(x) = d(x, 0) and wt(x + y) ≤ wt(x) + wt(y).
4.Prove that if x, y ∈ Z n 2 both have even weights then their sum x + y also has even weight.

5.For each of the following codes, fifind the minimum distance of the code and determine how many errors it can detect and correct.
(i) C1 = {0000, 1100, 1010, 1001, 0110, 0101, 0011, 1111} in Z42;
(ii) C2 = {10000, 01010, 00001} in Z 52 ;
(iii) C3 = {000000, 101010, 010101} in Z62.
Which of these codes can be extended by a further codeword without changing the minimum distance?
6.Construct a code in Z62 which can encode fifive messages and correct one error.
7.Consider the code Mathematics代写
C = {000000000, 100110110, 010011011, 001101101,
110101001, 101011101, 011110010, 111000111}.
Prove that C is not linear.
Determine the weights of the code-words.
Verify that the minimum distance is 3.
What are the error-detecting and error-correcting capabilities of C ?
8.Let C ⊆ Z72be the linear code with the generator matrix
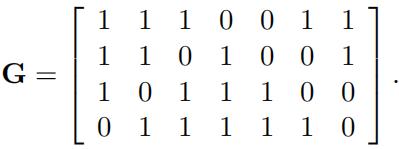
Find a parity check matrix for C , list all the code-words, and determine the error-detecting and error-correcting capabilities of C .
9.Let C ⊆ Z62 be the linear code with the parity check matrix Mathematics代写
Find a generator matrix for C
list all the code-words, and determine the error-detecting and error-correcting capabilities of C.
10. Let C ⊆ Zn2 be a linear code with a generator matrix G of dimension k × n . For each t ∈ {1, . . . , n} defifine Ct = {x1x2 . . . xn ∈ C : xt = 0} .
(i) Prove that each Ct is a linear code. Mathematics代写
(ii) Prove that either |Ct| = |C| or else |Ct| = |C|/2 .
(iii) Prove that if G has no column consisting entirely of zeros, then the sum of the weights of all of the code-words in C is equal to n · 2k−1 .
更多代写:Assignemnt代写 托福家庭版 Accountant会计网课代上价格 英国essay范文 澳大利亚研究性论文代写 MATH数学作业代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写