School of Mathematics and Statistics
MT4516 Finite Mathematics
Mathematics作业代写 Does there exist such a code which detects single errors? Does there exist a code D ⊆ Z72with 16 code-words which corrects single errors?
1.Let n = 2k + 1 be an odd number. Prove that C = {00 . . . 0, 11 . . . 1} ⊆ Zn 2 is a perfect k-error correcting code. (Hint:
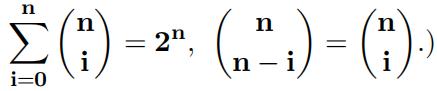
2.Prove that there does not exist a code C ⊆ Z72with 17 code-words which corrects single errors. Does there exist such a code which detects single errors? Does there exist a code D ⊆ Z72with 16 code-words which corrects single errors?

3.Prove that for every k > 0 and every n > 0 there exists a k-error correcting code C ⊆ Z n2 with at least Mathematics作业代写
code words. (Hint: Consider balls of radius 2k.)
4.Let ,
and
be the extended Hamming code, extended reversed Hamming code and the extended Golay code respectively, as defifined in
lectures.
(i) Let w ∈ be an arbitrary code-word, and write it as w = pqr, where each of p, q, r has length 8. If we defifine t = p + q + r, u = p + r and
v = q + r, prove that t ∈ , u, v ∈
.
(ii) By writing the word w = 111111000001101110110001 in the form w = pqr, prove that w∉ . Mathematics作业代写
(iii) Prove that 101111011001011000100100 ∈ .
5.Show that the number of n × n Latin squares is 1, 2, 12, 576 for n = 1, 2, 3, 4 respectively. Mathematics作业代写
6.Prove that the isotopy relation is an equivalence relation.
7.Prove that there is an 11 × 11 Latin square which cannot be obtained from the multiplication table of a group by permuting the rows, columns and entries. (Hint: You may use the fact that there is only one group of order 11. )
更多代写:金融Midterm代考 线上考试如何作弊 加拿大留学生代考价格 essay例子 论文润色价格 Mathematics代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写




