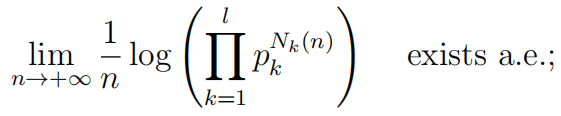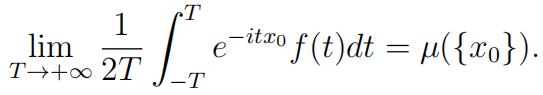Homework 2—Advanced Probability
Due Monday, April 20
高级概率作业代写 2.2(10points) Suppose limn→+∞ P[|Xn−X| > s] = 0 for any s > 0 and P[X = x] = 0. Show that P[{X ≤ x}O{Xn ≤ x}] → 0.
2.1(10points) If {Xn} is a sequence of independent and identically distributed v.’s not constant a.e., then P[Xn converges] = 0.
2.2(10points) Suppose limn→+∞ P[|Xn−X| > s] = 0 for any s > 0 and P[X = x] = 0. Show that P[{X ≤ x}O{Xn ≤ x}] → 0.
2.3(10 points) Let α be completely normal. Show that by looking at theexpansion of α in some scale we can rediscover the complete works of Shakespeare from end to end without a single misprint or interruption.

2.4(10points) For any sequence of v.’s {Xn}, (a) Xn → 0 a.e. would result in Sn/n → 0 a.e. (b) Xn → 0 in Lp would result in Sn/n → 0 in Lp for p ≥ 1. 高级概率作业代写
2.5(10points) Let {Xn, n ≥ 1} be a sequence of independent, identically distributed r.v.’s; also, let τ be a positive integer-valued v. that is independent of the Xn’s.
Suppose that both τ and X1 have finite second moments, then
σ2(Sτ ) = E[τ ]σ2(X1) + σ2(τ )(E[X1])2.
2.6(10points) Let {Xn, n ≥ 1} be a sequence of independent, identically distributed r.v.’s; also for some finite l, we have Σl pk = 1 where each pk ≡ P[X1 = k]. Let
Nk(n) be the number of values of j = 1, 2, …, n such that Xj = k. Show that
in addition, find the limit.
2.7(10points) Suppose that supn f dµn < +∞ for a nonnegative function f such that f (x) → +∞ as x → ±∞. Show that {µn} is tight. 高级概率作业代写
2.8(10 points) Let f be the ch.f. of the p.m. µ. For each x0, showthat
2.9(10points) Show that the f. for the standard normal Z is f (t) = e−t2/2. 高级概率作业代写
2.10(10 points) For a Poisson variable Yλsuch that P[Yλ = n] = e−λλn/(n!) for n = 0, 1, …, show that (Yλ − λ)/√λ ⇒ Z the standard Normal as λ → +∞.
更多代写:java代写 Gre代考 英国CS代写 艺术essay代写 学业论文代写 新加坡经济学网课代修