IEOR 4706 : Final
金融数学代考 Consider a discrete-time binomial model with T = 2 and R = 1 (meaning that the interest rate is constant equal to 0), u = 2 and d = 1/2.
Name :
SID :
1) Fix K2 > K1 > 0. A collar option with maturity T > 0, strikes K1 and K2, written on the underlying asset S, is an option with payoff at time T given by min(max(ST , K1), K2).
Assume that S does not deliver dividends and has no storage costs.
(a) Under no arbitrage condition, denote CLt(T, K1, K2, S) at time t ∈ [0, T] for the price of the collar option. Find an expression of CLt(T, K1, K2, S) in terms of K1, K2, d(t, T),Ct(T, K1, S) and Ct(T, K2, S).
(b) What purpose do you see for holding such an option ?
(c) Consider a discrete-time binomial model with T = 2 and R = 1 (meaning that the interest rate is constant equal to 0), u = 2 and d = 1/2. The initial risky asset price is S0 = 20. 金融数学代考
(c1) Are there arbitrage opportunity in this market ? Why ?
(c2) Give the price at time 0 of a collar option with strikes K1 = 8 and K2 = 20. Provide as well the replicating strategy.

2) Assume that there are T periods, and rt = (rt1, . . . , rtn) is the vector of returns of n financial assets at time t. The Kelly criterion consists of solving the problem
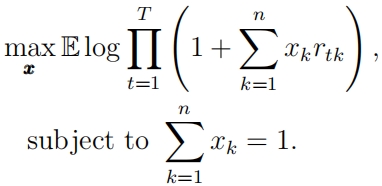
(a) Use Taylor expansion of log for approximation, and derive an explicit formula for the portfolio x = (x1, . . . , xn). Explain how this is applied for data.
(b) The data consists of the prices of Meta, Disney, Moderna and Netflix from 1/1/2022 to 11/30/2022. Taking T = 11 (one period corresponds to one month), compute the Kelly portfolio specified in (a). What is the annualized Sharpe ratio ?
(c) Compute the minimum variance portfolio of (b). What is the (in-sample) annualized Sharpe ratio ? Comment.
3) Consider the stochastic differential equation 金融数学代考
dZt = (2023 − log Zt)Ztdt + ZtdBt , Z0 = 1.
(a) Apply Itô’s formula to log Zt , and get an expression for Zt . Do you recognize log Zt ?
(b) Compute EZt and V ar(Zt). What are the limits of EZt and V ar(Zt) as t → ∞?
(c) What is the quadratic variation of Zt ?
4) Given a Black-Scholes financial market. Suppose f(t, St), a “price” at time t for a European type derivative with an expiration date T, is given as ,where σ is the volatility for the underlying asset, r is the risk-free interest rate, and St is the price of the underlying asset at time t.
(a) What is the payoff of this derivative at time T ?
(b) Is it an arbitrage free price ? Why ?
(c) Suppose T = 1 year, and suppose that the underlying price today is 5 dollars and the interest rate is 0 percent. If your portfolio is to long one unit of this derivative and short N(t) shares of the underlying. Find N(t) in terms of t and St so that the portfolio is risk-free.
5) Given a Black-Scholes financial market. Let r be the risk free rate, σ be the volatility,K be the strike and T be the maturity. The payoff function is given by [(ST − K)+] 2 . 金融数学代考
(a) Compute explicitly the price formula Ct(St , r, σ, K, T) for any t ≤ T. What is the replicating strategy ?
(b) Set r = 0.02, σ = 0.15, K = 100 and T = 1. Write down the Feynman-Kac PDE for the price v(t, x) at time t given the underlying stock price is x. Compute numerically v(0, x) for x ∈ {95, 96, . . . , 104, 105}, and compare with (a).
(c) As in (b), use the Monte Carlo method to compute v(0, x) for x ∈ {95, 96, . . . , 104, 105},and comment.
(d) Back to the standard Black-Scholes financial market, and the European option. The data consists of option trading for Apple on 10/19/2021. Plot the implied volatility sur-face, and what is the estimated implied volatility with strike 160 and maturity 1/7/2022 ?(This question should be treated separately to (a) – (c)).
更多代写:美国网课平台 gre在家代考 c++代码辅导 ASEssay代写 论文写作手法 商科金融代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写