MACM 201 – D100 AND D200 ASSIGNMENT #5
美国数学作业代做 Answer all questions on paper or a tablet using your own handwriting. Put your name, student ID number and page number at the top of each page.
Instructions
Answer all questions on paper or a tablet using your own handwriting. Put your name, student ID number and page number at the top of each page. If you use paper make a photo of each page and upload your solutions to crowdmark. If you use a tablet, export your assignment to .pdf and upload the .pdf to crowdmark.
Textbook Reading
- Sections: 9.1, 9.2, 9.3
Defifinitions, Concepts & Keywords
- Construct a generating function for a counting application.
- Find a formula for [x n]A(x) where A(x) is a rational GF.
- Use Wolfram Alpha or Maple to extract a coeffificient of a GF.
Exercises 美国数学作业代做
A.Textbook Questions
9.1 Exercises 2ac, 3.
9.2 Exercises 1de, 2bde.
9.3 Exercises 2ab, 3.
B.Instructor Questions
Questions on 9.1
1.Execute the following command in Wolfram Alpha:
Coefficient[ (x+xˆ2+xˆ3+xˆ4+xˆ5+xˆ6)ˆ6, x, 18 ]
to compute the coeffificient of x 18 in the polynomial (x + x 2 + x 3 + x 4 + x 5 + x 6 ) 6 .
Alternatively, if you have Maple, use the command
coeff( (x+xˆ2+xˆ3+xˆ4+xˆ5+xˆ6)ˆ6, x, 18 )
2.For each equation, express the number of integer solutions as the coeffificient of a polynomial.
Then use Wolfram Alpha or Maple to calculate the coeffificient. 美国数学作业代做
(a) a1 + a2 + a3 = 14 where a1, a2, a3 ≥ 0.
(b) b1 + b2 + b3 = 15 where 2 ≤ b1 ≤ 6, b2 is even and b3 is odd.
3.If a fair die is rolled 5 times, how many ways can the sum of the rolls equal 15?
Use a generating function. Use Wolfram Alpha or Maple to compute the required coeffificient.
4.Carol is collecting money from her cousins for a walkathon. Three cousins promise to give her either $2, $3, or $4 and one promises to give her either $5 or $10. Let an be the number of ways she can get $n. Give a generating function for an. How many ways can she get $15?

Questions on 9.2
5.Let A(x) = 1 − x + x 2 − x 3 + x 4 − . . . and B(x) = 0 + 1x + 2x 2 + 3x 3 + . . . .
Calculate rational GFs for A(x), B(x), A(x) + B(x) and B0 (x).
6.Let A(x) = 1 − x + x 2 − x 3 + x 4 − . . . . Let cn = [x n]A(x) 2 . Calculate a formula for cn.
7.Let an be the number of ways to select n balls from a large bag of red, blue, and yellow balls where the selection must include an even number of blue balls. Write down a generating func-tion for an in closed form.
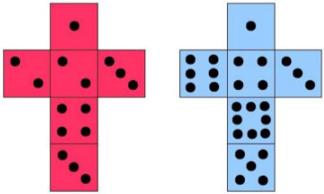
8.Consider the set of six sided die where one dice has the numbers 1, 3, 4, 5, 6, 8 and the other has the numbers 1, 2, 2, 3, 3, 4 (see fifigure).
If these two die are rolled at the same time we’ll investigate the possible sums and their frequen-cies in two ways: by direct enumeration in (a) and (b) below, and by using generating functions in (c) and (d) below.
(a) Determine the numbers which can occur as the sum of rolling these two dice.
(b) For each number in (a) determine the number of possible ways this sum could be rolled.
From this information, write down the generating polynomial D(x) for the sum when rolling these two die. 美国数学作业代做
(c) Now, write down the generating polynomial D1(x) for the fifirst dice, and D2(x) for the second dice.
(d) Verify that D1(x) · D2(x) = D(x) by multiplying the two polynomials in part (c).
(e) How does the generating polynomial D(x) compare to the one for the sum when rolling two standard six sided die?
9.Determine a formula for the coeffificient of x n for the rational GFs 1/(1 + 2x)3and x/(2 − x)3.
10.Find a rational GF for the sequence 0, 1, −2, 4, −8, 16, . . . .
11.Consider the generating function A(x) =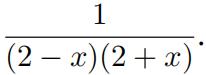
12.Let A(x) =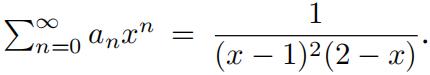
Questions on 9.3 美国数学作业代做
13.List all partitions of 7.
14.Find the generating function for the number of integer solutions of 2x + 3y + 5z = n for the cases
(a) x, y, z ≥ 0.
(b) x, y, z ≥ 1.
更多代写:劳动经济学网课代修 gmat代考被抓 经济学网课托管价格 Essay代写和辅导的不同 金融类paper代写 International Finance作业代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写