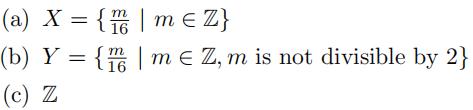MAT301, Problem Set 1
Due May 22 2019
留学生代写作业 Suppose that G is a group, and a and b are two arbitrary elements of G. Prove that there is a unique element c ∈ G so that ca = b.
Cayley tables
1.Write out a Cayley table for a group that has exactly 3 elements (make sure it satisfifies the properties of a group).
You must label one element (the identity) as e, but you are free to label the other two elements whatever you want.
Ask yourself (but you don’t need to write it) whether you could have done it any other way.
2.Write out the Cayley table for Z4, U(5), and U(12). All three groups have 4 elements. Would you say that any of them are the ”same”? We haven’t defifined this concept of ”sameness” thoroughly yet, but think about it.
Modular arithmetic 留学生代写作业
- Suppose that m is an integer and m ≡ 6 mod 12. What possible values of k satisfy k ≡ m mod 15? Explain why.
Give an example of such an m for each possible value of k ( mod 15).
- What values of x satisfy 3x + 2 ≡ 7 mod 13? What values of y satisfy 3y + 2 ≡ 11 mod 12? List all possible integers for each.

Groups
- Prove that if G is a group, and a and b are group elements such that ab = b, then a = e (e is the identity). Note:
this is a stronger statement than ”uniqueness of identity”.
- Suppose that G is a group, and a and b are two arbitrary elements of G. Prove that there is a unique element c ∈ G so that ca = b. (There are two things to prove here. First that there is such an element – existence – and that there is only one element that does this – uniqueness).
- Below I will give a short list of triples of a set, a binary operation on the set, and a distinguished element. Determine whether they form a group. If they do show that the 3 properties of a group are satisfified, and if they are not a group, show how it violates one of the properties of a group. 留学生代写作业
(a) Set: Z. Operation: addition of integers. Distinguished element: 1.
(b) Set: Q+ = { m n | m and n are positive integers}. Operation: multiplication of rational numbers. Distinguished element: 1.
(c) Set: {r ∈ R | r ≥ 1}. Operation: multiplication of real numbers. Distinguished element: 1.
Orders of elements
- List all of the elements of Z9. Write the order of each of them.
- Recall that in lecture we saw we can describe the dihedral group, Dn, as being generated by a rotation, r, and a reflflections, that satisfy rn = e, s2 = e, and srs = r−1 . Show that rks has order 2 for any k ∈ Z. Does this account for all of the elements of order 2? (hint: the answer will depend on n)
- Suppose that G is a cyclic group, and it contains an element of order 7. Can G have order 40? Can G have order35? Explain why.
- Suppose that G is a cyclic group, and it has an element of order 20, and an element of order 16. Prove that 80 divides |G|.
Subgroups: 留学生代写作业
12.Recall that the rational numbers are defifined as They form a group under addition,with the identity element 0. Consider the following subsets of Q. Which of them are subgroups with the given group operation? Use a subgroup test to determine this.
13.Draw the subgroup lattice of Z6 and Z18.
Equivalence relations and partitions (if you are having diffiffifficulty I suggest consulting section 0 of Gallian)
14.Recall that a relation on a set, X, is a rule that says whether two elements of that set are ”related” in some way.
We write x ∼ y if x and y are related by the relation ∼, and x y if they are not. In general, it depends on the order we write it in, it may be the case that x ∼ y but y x. For example < is a relation, but 1 < 2, and 2 ≮ 1.
An equivalence relation, ∼ is a relation that is:
- reflflexive: x ∼ x for all x ∈ X,
- symmetric: if x ∼ y, then y ∼ x for all x, y ∈ X,
- transitive: if x ∼ y, and y ∼ z, then x ∼ z for all x, y, z ∈ X. 留学生代写作业
(a) Show that < is not an equivalence relation on R.
(b) Show that equality mod n is an equivalence relation on Z. (recall that x ≡ y mod n if x − y is divisible by n).
-
Prove that any given integer, m is equal mod n to one of 0, 1, 2, . . . , n − 1. Hint: there is a least possible integer k such m − kn > 0 – what will m − kn be in this case?
- A partition of a set X is a collection (a set) of subsets of X, such that every element of x is an element of exactly one of the subsets. For example, {{1, 2}, {3}, {4, 5}} is a partition of the set {1, 2, 3, 4, 5} (note it is a set of sets).
The collection of subsets {{1, 2}, {4, 5}} do not constitute a partition as 3 is not contained in one of them, and the collection {{1, 2, 3}, {3, 4, 5}} also do not constitute a partition as 3 is contained in more than one of them. 留学生代写作业
Given a positive integer, n, let [k]n denote the subset of Z, [k]n = {m ∈ Z | m ≡ k mod n}.
Using the result of the above problem, prove that {[0]n, [1]n, [2]n, . . . [n − 1]n} is a partition of Z.
17.Describe how you can get a partition from an equivalence relation, and vice versa. The previous question is an example of this. For this question don’t worry about being very formal, but try to communicate the idea as concisely and fully as you can.
更多代写:Psychology代写 在家考托福作弊 新加坡Course代写 PS申请信代写 Report范文 gre远程代考
合作平台:essay代写 论文代写 写手招聘 英国留学生代写