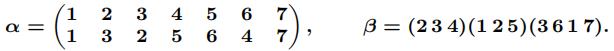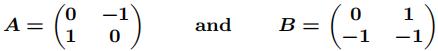School of Mathematics and Statistics
MT4003 Groups
Problem Sheet I: Defifinition and Examples of Groups
理科数学作业代写 Let F5 = {0, 1, 2, 3, 4} be the fifield of order 5, where addition and multiplication are calculated modulo 5. You may assume that F5 is a fifield.
1.Consider the following two permutations from the symmetric group S7 of degree 7: 理科数学作业代写
Write each of the following permutations as products of disjoint cycles: (i) α; (ii) β; (iii) αβ;
(iv) βα; (v) α−1; (vi) β−1; (vii) (αβ)−1; (viii) β−1α−1.
2.Show that the symmetric group Sn is non-abelian if and only if n > 3. 理科数学作业代写
3.Let F5 = {0, 1, 2, 3, 4} be the fifield of order 5, where addition and multiplication are calculated modulo 5. You may assume that F5 is a fifield.
Consider the general linear group GL2(F5), more often denoted by GL2(5).
(a) For 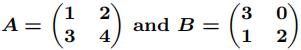
(b) Prove that GL2(5) is non-abelian.
(c) Determine the order of GL2(5).
[Hint: A matrix is invertible if and only if its rows (or, equivalently, columns) are linearly independent. How do you choose a linearly independent pair of vectors from F25?]
4.Let F be an arbitrary fifield. Show that the general linear group GLn(F ) is non-abelian if and only if n ≥ 2. 理科数学作业代写
5.Verify that the Klein 4-group is indeed a group.
[Do not check each of the 64 cases for associativity. Instead, use careful thought to reduce how many checks you need to perform.]
6.Consider the following three matrices with entries from the complex numbers:
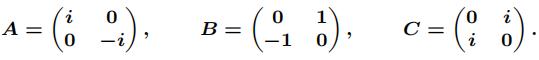
(a) Let G = {I,-I,A,-A, B,-B,C,-C}, where I denotes the usual 2 × 2 identity matrix. Cal-culate a multiplication table for G and hence show that matrix multiplication defifines a binary operation on G.
(b) Deduce that the quaternion group is indeed a group.

7.Let G be a group and a be an arbitrary (but fifixed) element of G. Defifine a mapping τa : G →G by xτa = a−1xa for each x ∈ G. (This mapping is called conjugation by a.)
(a) Specialise (for this part only) to the case G = S3 and a = (1 2 3). Compute στa for each σ ∈ S3.
(b) Prove that τa is always an isomorphism (in any group).
(c) If G is an arbitrary group, fifind an element a ∈ G such that τa is the identity mapping (that is, xτa = x for all x ∈ G).
(d) Prove that G is abelian if and only if all the mappings ⌧a are equal to the identity mapping.
8.Let G, H and K be groups. 理科数学作业代写
(a) If Ø: G → H is an isomorphism, show that its inverse Ø−1 : H → G is also an isomorphism.
(b) If Ø: G → H and : H → K are isomorphisms, show that Ø : G → K is also an isomorphism.
(c) Show that ≅ (being isomorphic) is an equivalence relation on the class of all groups.
9.Let G be a group and defifine a mapping φ: G → G by xØ = x−1 for each x ∈ G.
(a) Prove that Ø2 (= ØØ) is the identity mapping.
(b) Prove that Ø is a bijection.
(c) Prove that Ø is an isomorphism if and only if G is abelian.
(d) Suppose that G is a fifinite group of even order. Prove that there exists a ∈ G of order 2.
10.Let G be any group. If x ∈ G, prove that (x−1)−1 = x. 理科数学作业代写
11.Let G be a group and suppose that x2 = 1 for all x∈G. Show that G is abelian.
12.Let G be a group and let a, b ∈ G. Prove that if a2= 1 and b2a = ab3, then b5 = 1.
[Hint: b4 = b2b2aa, b6 = b2b2b2.]
13.Let G be a group.
(a) Prove that for any x, y ∈G, the following formulae involving the order of an element hold: 理科数学作业代写
o(x) = o(x−1); o(x) = o
(y−1xy), and o(xy) = o(yx).
(b) If σ is a permutation in Sndecomposed as a product of disjoint cycles as σ = σ1σ2 … σk, where σi is a cycle of length ri, then prove that
o(σ) = lcm(r1, r2,…,rk).
(c) Consider the matrices
from the general linear group GL2(Q). Show that o(A) = 4, o(B) = 3, but that AB has infifinite order.
更多代写:加拿大哲学代考 线上考试作弊技巧 澳大利亚econ Midterm代考 essay outline写作 cs论文修改代写 Mathematics代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写