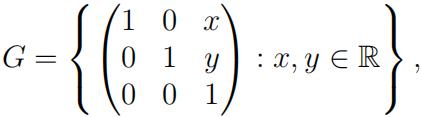INTRODUCTION TO GROUP THEORY
MATH10010
(Paper code MATH–10010)
数学代写价格 On this examination, the marking scheme is indicative and is intended only as a guide to the relative weighting of the questions.
This paper contains two sections: Section A and Section B.
Each section should be answered in a separate booklet.
Section A contains FIVE questions and Section B contains TWO questions
All SEVEN answers will be used for assessment.
Calculators are not permitted.
Candidates may bring four sheets of A4 notes written double-sided into the examination.
Candidates must insert these into their answer booklet(s) for collection at the end of the examination.
On this examination, the marking scheme is indicative and is intended only as a guide to the relative weighting of the questions.
Section A: Short Questions 数学代写价格
A1. (a) (6 marks) For the set and binary operation in each of (i) and (ii), state which of the axioms of a group are and are not satisfified. No explanations are necessary.
(i) The set of rational numbers Q with the binary operation of multiplication.
(ii) The set of natural numbers Z>0 with the binary operation of addition.
(b) (2 marks) Give an example of a set with a binary operation that is not associative;no explanation is necessary.
A2. (a) (4 marks) Suppose G is a multiplicatively written group with identity element e, and x, y ∈ G. Carefully using the defifinition of a group, show that if xyx = x 2 then y = e. 数学代写价格
(b) (4 marks) Show that H = {2 i : i ∈ Z} is a subgroup of (R>0, ×).
A3. For n ∈ Z>0, let Un be the multiplicative group of congruence classes [a] ∈ Z/nZ for which hcf(a, n) = 1.
(a) (4 marks) Show that [17] ∈ U40, and fifind its inverse.
(b) (4 marks) What is the order of U40? Is 175 ≡ 1(mod 40) true or false? Explain.
A4. (a) (4 marks) Write the element
(1, 3, 2, 4, 9, 8, 5)(1, 2)(4, 8, 6)(2, 9, 3)
of the symmetric group S9 as a product of disjoint cycles and compute its order.
(b) (4 marks) Is the alternating group A4 abelian? Explain.
A5. (a) (4 marks) Let D10be the dihedral group of order 10, with standard elements a, b.
Write ab2a7ba4 in the form ai or ai b for some 0 ≤ i < 5.
(b) (4 marks) Let D20 be the dihedral group of order 20, and let C5 = h ci be a cyclic group of order 5 with generator c. Is the function f : D20 → C5 defifined by
f(ai) = c i , f(ai b) = ci
a homomorphism? Explain.

Section B: Longer Questions 数学代写价格
Please use a new booklet for this Part.
B1. (a) (7+5 marks) Consider the set of matrices
with binary operation given by matrix multiplication ·.
(i) Show that (G, ·) is an abelian group.
(ii) Show that (G, ·) is isomorphic to the group (R 2 , +).
(b) (5 marks) Find 0 ≤ a < 23 so that 350 ≡ a(mod 23) using Fermat’s little theorem or otherwise.
(c) (5 marks) If an element x of a group G has order 30, what is the order of x 18?
(d) (5+3 marks) Suppose G, H are (multiplicatively-written groups) and x ∈ G, y ∈ H have fifinite order.
(i) Show directly that (g, h) ∈ G × H has fifinite order.
(ii) If g and h each have order at most 10, what is the largest possible order of (g, h)? 数学代写价格
B2. (a) (4+3 marks) Let R≠0be the group of non-zero real numbers under the operation of multiplication. Defifine f : R≠0→ R≠0 by f(x) = |x|, the absolute value of x.
(i) Show f is a homomorphism.
(ii) State the consequence of the homomorphism theorem applied to f.
(b) (5+5 marks) Let G = (R>0, ·) be the group of positive real numbers under multipli-cation, and let X = R. Defifine g · x = gx for g ∈ G and x ∈ X, where gx is the usual
multiplication of real numbers.
(i) Show that g · x = gx defifines an action of G on X.
(ii) Describe the orbits and stabilizers of this action.
(c) (4+4 marks)
(i) Give an example of a subgroup H of a group G that is not normal, with a brief explanation.
(ii) Suppose H is a subgroup of a group G with the property that for any x ∈ G,there exists y ∈ G so that xH = Hy. Show that H is a normal subgroup of G.
(d) (5 marks) Suppose G is a group of order 50 that acts on a set X of size 4, with g · x ≠x for some g ∈ G and some x ∈ X. Show that G must have a subgroup of
order 25.
更多代写:北美市场营销学代写 gre在家考作弊 北美法律作业代写 harvard格式指南 论文写作格式 算机论文作业代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写