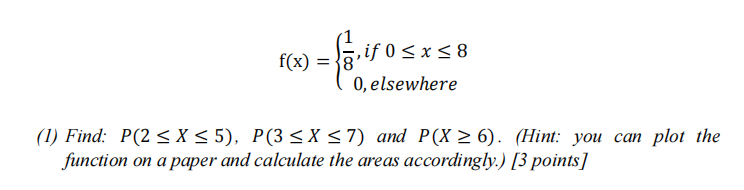CE262-5 Final Assignment
工程数学代写 Final assignment (submission deadline 12/Jan/2021 11:59:59) 2020-2021Where to submit: FASERENGINEERING MATHEMATICSCandidates must answer ALL ···
School of Computer Science and Electronic Engineering 工程数学代写
Final assignment (submission deadline 12/Jan/2021 11:59:59) 2020-2021
Where to submit: FASER
ENGINEERING MATHEMATICS
Candidates must answer ALL questions.
The final assignment consists of questions for Probability, Fourier/Laplace transform.
The final assignment is worth 40% of the total assessment for this module.
You are free to refer to the lectures and labs, but this assignment must be your own work.
Please make sure you only submit word or pdf file, in particular, if you are using Apple system, please transform it to word or pdf format before submission to FASER.
-
Probability: 工程数学代写
1.1 Infectious disease poses severe public threat, and one may get infected if he/she goes to public area without a proper protection. Suppose that in one trial (i.e. goes to public area once) if he/she follows the government rules the probability of being infected is low: ?f = 0.01; and if he/she breaks the government rules the probability of being infected is high: ?b = 0.1.
Please solve the following questions based on what you have learnt in probability, please present the detailed derivation for the solution step by step (you can do the calculation by using MATLAB on your own computer or CSEE virtual lab, check out the link on Moodle CE262 for the virtual lab).
(1)one goes to public area for 20 times, if he/she follows the government rule in each time, what is the probability of NOT being infected? and what is the probability of being infected, where “being infected” means being infected “at least once”; [3 points]
(2) one goes to public area for 20 times, if he/she breaks the government rule in each time, what is the probability of NOT being infected? and what is the probability of being infected, where “being infected” means being infected “at least once”; [3 points]
工程数学代写
(3) what is the ratio of the probability of NOT being infected in one trial for “following the government rule” over “breaking the government rule”: i.e. ?????? = ???? ??????; based on the results in (a) and (b) calculate what will the above ratio become when the number of trial is 20: ??????? = ???? ??????. And what conclusion can be draw by comparing the ratios between one trial and 20 trials. [5 points]
1.2 A sequence of bits are transmitted over an error-prone channel, which inverts any bit sent over it with a probability p=0.05.
(1) what is the probability that the first transmission error occurs with the tenth bit sent? [3 points]
(2) what is the expected number of bits being transmitted when the first transmission error occurs? Please derive the results step by step. [3 points]

(2) Determine and plot the graph of the cumulative distribution function ? of ?. You can either plot it by using MATLAB or draw by hand and put into the word document. [3 points]
-
Fourier transformation 工程数学代写
2.1 Use the Fourier Transform ??{????(?)} = ????(?) and the time-shift property of the Fourier transform, to find the Fourier transforms of the pulses ?1(?) and ?2(?), whose graphs are shown below.
(1) You are required to first write down the time-shift property of the Fourier transform [2 points]
(2) and then calculate ??{??(?)} and ??{??(?)} step by step [4 points]
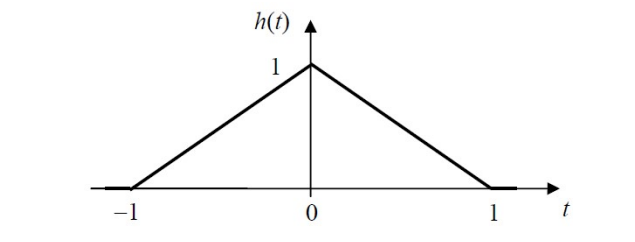
2.2 The graph of a triangular pulse, ℎ(?), is shown in below figure
(1) Express the derivative ??(?)
__ in terms of the pulses ??(?) and ??(?) in 2.1.
??
Using this representation, and the time-derivative property of the Fourier transform, find the Fourier transform of ℎ(?). [3 points]
(2) You are required to first write down the time-derivative property of the Fourier transform; [2 points]
(3) And then calculate ??{?(?)} step by step (Hint: express your answer in terms of the sinc function). [5 points]
3 Laplace transform 工程数学代写
3.1 Find the inverse Laplace transform of ?(?) = , please derive it step by step including the partial fraction and then inverse Laplace transform. [5 points]
3.2 Introduction of Wien bridge circuit
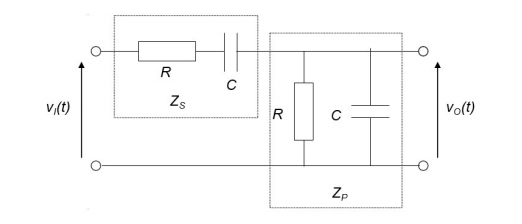
The Wien bridge circuit comprises two equal resistors and two equal capacitors, as shown in Figure 2.1.
Figure Wien Bridge circuit
Now re-draw the circuit, replacing the components by their Laplace impedances, and the input and output voltages by their Laplace transforms, VI(s) and VO(s), respectively.
(1) Find the Laplace impedance, ZS(s) of the series R-C combination (see, above Figure Wien Bridge circuit for ?௦) [2 points]
(2) and find the Laplace impedance, ZP(s) (see above Figure), of the parallel R-C combination, derive your results step by step: [2 points]
(3) The (Laplace) transfer function of the circuit can be then found from the voltage divider rule. Now use your calculations of ZS and ZP to write down the transfer function, H(s), in rational form, i.e. as the ratio of two polynomials in s. [5 points]
工程数学代写
Hint: your answer should depend on the component values only through the productRC (check whether you are correct or not). This has dimensions of time, and determines where on the frequency scale the bridge circuit has significant features (lower and upper cut-off frequencies, etc.). For the remainder of this activity, we shall assume that RC = 1 second. The significant features of the transfer function H(s) will then be close to 1 Hz. Significant features close to (for example) 1 MHz could be obtained by setting RC to 1 microsecond.
3.3 Impulse response
(1) Use the ‘b2 -4ac’ formula (https://www.mathsisfun.com/algebra/quadratic-equation.html) to find the poles of the Wien bridge circuit. (These are the roots of the denominator of the transfer function, when expressed in rational form.) [2 points]
(2) Make a sketch of the complex s-plane, and plot on it the positions of the poles and zeros of H(s). Please plot them by using MATLAB, which we have learnt in the lab session, also state which ones is poles and which ones are zeros (we have learnt how to add text to a figure). [3 points]
(3) Use the technique of partial fractions to express the transfer function in the form 工程数学代写
(4) and hence find the impulse response, h(t), of the circuit, write down the function of h(t) against time [3 points]
(5) Which types of complex exponential does it include? [2 points]
(6) How are these related to the positions of the poles in the s-plane? (Hint: you may refer to Lab 2 to answer questions d and e). [2 points]
(7) Write some MATLAB code to plot a graph of h(t) against t, write down your code and also include the figure results. [3 points]
(8) Is the circuit stable? (You can answer this question by inspecting the poles or the time-domain response) [2 points]
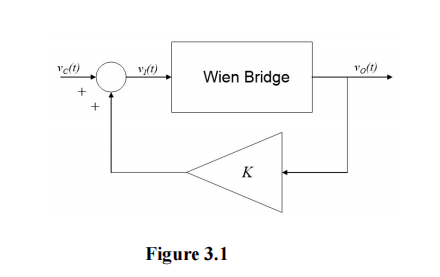
3.4 The closed-loop transfer function for “Wien bridge with feedback” The Wien bridge circuit is combined with an operational amplifier in the positive (be careful) feedback arrangement of Figure 3.1.
工程数学代写
(1)Re-draw this arrangement in the Laplace domain, and calculate the closed-loop transfer function, in rational form. Your answer should be expressed in terms of K. [5 points]
(2) Find the poles of the closed-loop system for the following values of K, you may use ‘b2 -4ac’ formula to calculate roots.
(i) K = 1; (ii) K = 2; (iii) K = 3; (iv) K = 4. [4 points]
3.5 Impulse response of the closed-loop system
(1) For the value of the amplifier gain K=3, use the technique of partial fractions to express the closed-loop transfer function in the form
(2) And hence find the impulse response, g(t), of the closed loop system, write down g(t) with respect to time t. [3 points]
(3) Which types of complex exponential does it include? How are these related to the positions of the poles in the s-plane? (hint: you may refer to Lab 2 to answer this question) [2 points]
(4) Write some MATLAB code to plot a graph of g(t) against t. write down both the code and also include the figure results. [3 points]
(5) What conclusions can you draw about the behavior of the closed-loop system for this value of K? [2 points]
The total mark is 100%.
更多代写:Haskell编程代写 生物学代考 lab代写 essay代写 英国代写 C++作业代写