comp2022/2922
Assignment 3 – SAT encodings and CFGs
北美计算机代写 You will be evaluated not just on the correctness of your answers, but on your ability to present your ideas clearly and logically.
This assignment is due in week 8 on Sunday 10 October 11:59pm Gradescope will say Sunday11 October 12:00am
All work must be done individually without consulting anyone else’s solutions in accordance with the University’s “Academic Dishonesty and Plagiarism” policies.
You will be evaluated not just on the correctness of your answers, but on your ability to present your ideas clearly and logically. You should always justify your answer unless explicitly asked not to do so. Your goal should be to convince the person reading your work that your answers are correct and your methods are sound. For clarifications and more details on all aspects of this assignment (e.g., level of justification expected, late penalties, repeated submissions, what to do if you are stuck, etc.) see the Ed post “Assignment Guidelines”.
What to submit:
- Submita pdf on GS with all your answers (excluding your implementations).
- Submitthe solutions to Problem 1,3, and 4 on Ed Lessons.
- Submit your code for Problems 2 and 5 on Ed Lessons. The implementation part of the assignmentwill be autograded based on hidden input/output test
Problem 1. (6 marks) 北美计算机代写
Write each of these formulas in CNF, and say in as few words as possible what they express (e.g., x y expresses that ”x and y agree on their truth-values”).
- 1. x → ¬(y ↔z).
- 2. x ↔(y ↔ z)
For each item, 1 mark for the CNF formula (no derivation needed), 2 marks for succinctly saying what it expresses.
Problem 2. (19 marks)
You work for CliqueFinder, a company that mines social-networks for cliques. A social-network is modeled by an undirected graph G = (V, E). For instance, ver- tices may represent people and edges may represent the ”are friends” relation. A clique of G is a subset C V of the vertices such that every pair of different vertices in C are related by an edge. For instance, a clique may represent a group of people who are all friends with each other. See the appendix for a refresher on graph concepts.
Clients are interested in decomposing their networks into cliques. So, you define the following computational problem that you call the exact-clique-cover (ECC) problem. An input instance of the ECC problem consists of V, E, K where (V, E)is an undirected graph and K is a natural number with 1 ≤ K ≤ |V|. Given an instance, the ECC problem asks (a) to say if there is a partition V = ∪K Vi of the vertices into K non-empty parts, such that each part Vi is a clique of G, and(b)ifthere is such a partition, to return one such partition, called a solution. 北美计算机代写
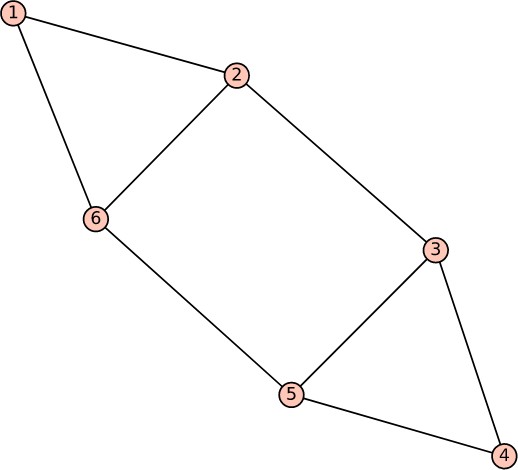
For example, consider the graph (V, E) pictured:
If K = 1 then the instance V, E, K has no solution; if K = 2 then the instance V, E, K has a solution, e.g., V1 = {1, 2, 6} and V2 = {3, 4, 5}1; if K = 3 then the instance V, E, K has solutions, e.g., V1 = {1, 2, 6}, V2 = {3, 5} and V3 = {4}; and similarly if 4 ≤ K ≤ 6 then the instance V, E, K has solutions.2
You remember studying how to encode facts and reasoning into logic, and so you decide to see if you can encode this problem into logic and use a SAT solver to solve it.
For concreteness you should assume that the vertex set V is of the form {1, 2, · · · , N} for some N ≥ 1. 北美计算机代写
Your plan is to reduce the ECC problem to the satisfiability problem for CNF formulas. Namely, find an encoding of an instance V, E, K by a CNF formula ΦV,E,K such that:
- thereis a solution to the instance V, E, K iff the formula ΦV,E,K is satisfiable,
- you can convert every satisfying assignment of ΦV,E,Kinto a solution for the instance V, E, K,
- and the size of ΦV,E,Kis bounded by a polynomial in N, K.
Explain what your encoding is and why it is correct. To do this, you should:
- (12 marks) State all the variables you introduce, and say in plain language what they are supposed to represent. It should be clear from your de- scription how an assignment encodes a solution. State all the clauses you introduce,and justify each with a short sentence in plain language saying what it captures. For full credit , the size of your formula ΦV,E,K should be bounded above by a polynomial in N and K.
1Actually, the only other solution with K = 2 swaps the order, i.e., V1 = {3, 4, 5} and V2 ={1, 2, 6}
2 K = 1 asks if the graph itself is a clique; and K = N always has solutions, i.e., each vertex is in its own part.
For the level of justification and the formatting, look at the solutions to similar problems in Tutorial 4, i.e., problems 15 and 16.3
- (2 marks) Find an asymptotic upper bound on the size of your encoding formula ΦV,E,Kin terms of N and K, and write it in big-Oh notation. You can assume that each variable can be stored in constant space.
Implement your encoding using the specified file formats (the formats are de- scribed below). To do this you should:
- (4 marks) Write a program that takes as input an instance V, E, K (in the GRAPH format) and returns its encoding formula ΦV,E,K(in the DIMACS formula format).
- (1 mark) Write a program that takes as input (i) an instance V, E, K (in the GRAPH file format), and (ii) an assignment of the variables (in theDIMACS assignment format), and returns the solution that the assignment encodes (in the ECC format). 北美计算机代写
Here is a refresher of basic terminology about graphs:
- An undirected graph G is a pair (V, E) where V is a non-empty finite set of vertices and E V V is an irreflexive symmetric relation of edges. Irreflex- ive means that for every u V, (u, u) E, and symmetric means that for every u, v V, if (u, v) E then also (v, u) E. In other words, there are no self loops, and edges are not directed.
- Aclique (aka complete-graph) is a subset C ⊆ V of the vertices such that (x, y) ∈ E for all x, y ∈ C with x ƒ= y.
- Note that although the empty set of vertices C = ∅ V is a clique, the cliques that make up a solution to the ECC problem are required to be non-empty.
Problem 3. (6 Marks) Consider the following CFG G: 北美计算机代写
S → AT | c
T → TA | BT | c
A → a B → b
- (1 Mark) List the variables.
- (1 Mark) List the terminals.
- (2 Marks) Find a regular expression R such that L(R) =L(G).
- (2 Marks) Show that the grammar is ambiguous by giving two leftmost derivations of the same string.
3Make sure you have the latest version of Tutorial 4 from Ed since it was re-organised in week 6.
No additional justifications are needed.
Problem 4. (4 Marks) Sep 24: There was an error in this question. It is now fixed.
Let L be the language over the alphabet Σ = {a, b, c} consisting of all strings of the form ucv where u ∈ {a, b}∗, and |v| is the number of a’s in u.
For example, the following strings are in L: c, bbbc, aacbb, babbacab, abaccc, and the following strings are not in L: c, aabb, baacbba, aabcaab, abbacccc.
Here is a grammar G that generates the language L:
S → missingstring (1)
T → a | b | c (2)
B → Bb | c (3)
- (2 marks) Fill in the missing string. The string can mention terminals, vari- ables, and up to one|.
- (2 marks) Give one or two sentences explaining your answer.
Problem 5. (15 Marks) 北美计算机代写
Implement a program that given a CFG G = (V, Σ, R, S) in CNF and a string u Σ∗ as input, returns the number of leftmost derivations of u by the grammar G. Note that this number could be 0.
- Input: is a context-free grammar in Chomsky normal-form followed by a sequence of input strings. Input is read from standard input(stdin).
- Output: One line per input string, giving the string, a comma, and then the number of leftmost derivations.
Examples of usage, and of input and output are provided below.
Marks are assigned based on the proportion of test-cases that are passed.
A Appendix: Input/Output for the encoding problem 北美计算机代写
GRAPH file format
GRAPH is a file format for instances of the ECC problem. Here is a typical GRAPH file:
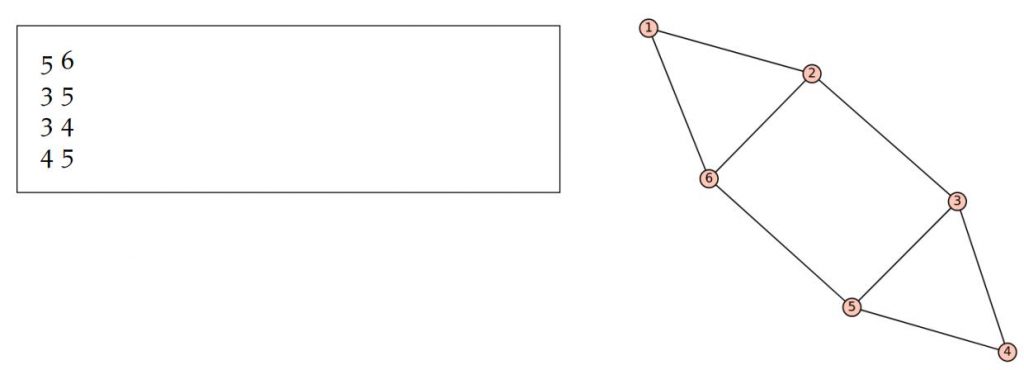
The file corresponds to the pictured graph, as well as the fact that the number of desired cliques is 2.
The format is as follows. At the top you can have comment lines that start with a ”c”, like this: c This line is a comment.
Then comes the problem line, which starts with a ”g” and then states the number of vertices, then number of edges, and the desired clique-cover size. In the example, there are N = 6 vertices, 8 edges, and K = 1.
Finally, the edges are listed. Each edge is represented as a pair of numbers i, j such that 1 i < j N. For instance a line with 3 5 says that there is an undirected edge between vertex 3 and vertex 5.

ECC file format
ECC is a format for solutions of the exact-clique-cover problem. Here is a typical ECC solution file:

The first line lists the number of cliques. This is also the number of remaining lines. Each successive line is a list of vertices. This file says that the two disjoint cliques that cover the vertices are the sets V1 = {1, 2, 6} and V2 = {3, 4, 5}.
If there is no solution, then the solution file should be
DIMACS formula format
DIMACS is a file format for CNF formulas. Here is a typical DIMACS formula file:

This file corresponds to the following formula over variables x1, x2, x3, x4, x5:
(x1 ∨ ¬x5 ∨ x4) ∧ (¬x1 ∨ x5 ∨ x3 ∨ x4) ∧ (¬x3 ∨ ¬x4)
The format is as follows. At the top you can have comment lines that start with a ”c”, like this: c This line is a comment.
Then comes the problem line, which starts with a ”p” and then says how many variables and clauses there are. For instance, here is a problem line that says this is a CNF problem with 5 variables and 3 clauses:
p cnf 5 3
Finally the clauses are listed. Each clause is represented as a list of numbers like 3 and -4. A positive number like 3 represents a positive occurrence of variable 3. A negative number like -4 represents a negated occurrence of variable 4. The number 0 is treated in a special way: it is not a variable, but instead marks the end of each clause. This allows a single clause to be split up over multiple lines.
DIMACS assignment format
DIMACS is also a file format for assignments in propositional logic. Here is a typical DIMACS assignment file:
It says that the formula is satisfiable, and a satisfying assignment maps x1, x4, x5 to 1 and x2, x3 to 0.
If you run ”minisat formula answer” where ”formula” is a DIMACS formula file, minisat will produce a DIMACS assignment file called ”answer”. If the formula is not satisfiable, then the ”answer” file will be

B Appendix: Input/Output for CFG problem 北美计算机代写
The input is a sequence of lines:
- A comma separated list of variablesymbols
- A comma separated list of terminalsymbols
- The startvariable
- One or more lines of theform:
- A -> BC
- A ->a
- A ->epsilon
- The stringend
- Oneor more lines, each consisting of a non-empty input
- The stringend.
The output is a sequence of lines, one for each of the input strings, with a number, i.e., the number of leftmost derivations of that input string by the grammar.
For example:
represents the grammar:
(T) → (A) (B) | (B) (A) | (S) (S) | (A) (C) | (B) (D) | c
(S) → (A) (B) | (B) (A) | (S) (S) | (A) (C) | (B) (D)
(C) → (S) (B)
(D) → (S) (A) (A) → a
(B) → b
and input strings ab, a, abab. and the expected output is

because ab has one leftmost derivation, a has no leftmost derivations, and abab has two leftmost derivations.
更多代写:北美工程代写 Gmat代考 英国Politics代写 北美金融essay代写 传媒论文代写 毕业论文代写到底靠不靠谱