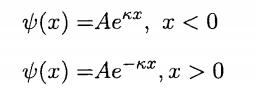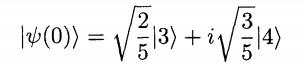Faculty of Arts and Science
DECEMBER EX AMIN ATIONS 2017
PHY 356F
Duration – 3 hours
加拿大物理代考 One of the possible values obtained in a measurement of A is√2μ. What other possible values can be obtained in a measurement of A?
Examination aids: One Handwritten 8.5″x11”Aid Sheet Allowed (both sides)
The exam is out of 90 marks. There are four questions. Total Pages=3.
Please read each question thoroughly before answering. Unsupported answers will only receive partial credit (i.e. show your work!)
Some possibly useful formulas are given at the end.
1. [20 marks/ A Three -State System 加拿大物理代考
Consider a three state system where the Hamiltonian and an observable A are given by the matrices
(a) One of the possible values obtained in a measurement of A is√2μ. What other possible values can be obtained in a measurement of A?
(b) Does a state exist in which both the results of a measurement of the energy and the observable A can be predicted with certainty? Why or why not? (Be quantitative in
your explanation.)
(c) Two measurements of A are carried out, separated by a time t. If the result of the first measurement is√2μ, determine the expectation value for the second measuremnent. Find the probability of each of the possible measurements, and show that this is consistent with your calculated expectation value.
2. [20 marks] A Bound State in One Dimension 加拿大物理代考
A particle of mass m in the potential V(x) =一Voδ(x) has a single bound state with energy E=and a wave function
where A is a normalization constant,andConsider a particle in this bound state.
(a) Evaluate the constant A in terms of k.
(b) Show without any calculation that (X> = 0. Calculate (x2). 加拿大物理代考
(c) Evaluate the expectation value of the potential energy in the bound state.
(d) Express the expectation value (P2) as an integral over x, and evaluate it to find (P2).
(e) Find the wave function of the particle in momentum space, ψ(p), and use your result to show without any calculation that (P) = 0.

3. [20 mark:s] The Simple Harmonic Oscillator in a Superposition of States 加拿大物理代考
At t = 0 a one dimensional simple harmonic oscillator with frequency w is in a linearcombination of the energy eigenstates
where the state |n〉 refers as usual to the n’th excited state of the harmonic oscillator.
(a) Find the expectation value of the momentum P at any timet > 0.
(b) Find the expectation value of P2 at any time t > 0.
(c) Find the product OXAP for this state as a function of t (again, for t> 0).
4. [30 marks] Angular Momentum and the Hydrogen Atom 加拿大物理代考
(a) Consider a system with total angular momentum j = 1/2. Denote the eigenstates of J2 and Jz by |j;, m), as usual.
i. Find the eigenstates and eigenvalues of the operators Jy and Jx + Jy.
ii. Suppose a measurement of Jx + Jy is made, and the system is found to be in the eigenstate with the larger eigenvalue. If Jy is measured immediately after, what is the probability of finding the value
(b) The wave function of a particle in a spherically symmetric potential is given by
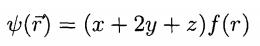
where If Lz is measured, give the possible results and the probability for each result.
(c) An electron in a hydrogen atom has the wavefunction
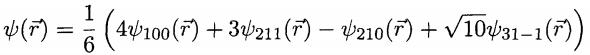
where the ψnlm are the usual energy and angular momentum eigenstates of the hydrogen atom.
i. What are the possible energies (expressed in terms of the ionization energy Ei) that can be measured and what are the probabilities of each? 加拿大物理代考
ii. Suppose the energy of the state is measured to be – Er/4. What is the state of the electron immediately after the measurement?
iii. Find the expectation values of L2 and Lz in the state
iv. Find the expectation value of Lx in the state
POSSIBLY USEFUL FORMULAS:
更多代写:哲学代写ASSIGNMENT gre在家考vpn 英国统计代上网课 经济Essay代写 建筑学博士论文代写 Essays代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写