ECMT5001: Final Examination (2022s1)
Econometrics代考 The total score of this exam is 60 marks. Attempt all questions. Correct all numerical answers to 2 decimal places.
The total score of this exam is 60 marks. Attempt all questions. Correct all numerical answers to 2 decimal places.
1.[Total: 20 marks] Bob, the proud owner of ìHungry Bob,î wanted to study how the fast food restaurantís revenue is related to customersí satisfaction. Econometrics代考
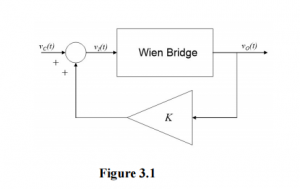
He collected data on daily revenue R (in $1,000) and customer satisfaction score S (in percentage points) over time, and ran a simple linear regression of R on S. He obtained the following regression result (standard error in parenthesis).
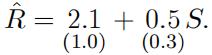
(a) [3 marks] Interpret the intercept term.
(b) [3 marks] Interpret the slope coe¢ cient.
(c) [4 marks] Let D denote the customer satisfaction score recorded in decimal points,i.e., What is the estimation result of a regression of R on D based on the same data? Your answer should be in the following form (standard error in parenthesis): Econometrics代考
(d) A competing restaurant ìBurger Queenî was opened next door. Let I denote the time dummy which equals 1 when Burger Queen was open, and 0 otherwise. To take this into account, Bob considered the regression as follows:
Using a sample spanning 80 days, Bob estimated the regression. The result is dis-played below (standard error in parenthesis):
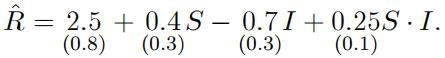
i.[5 marks] Bob suspected that the presence of Burger Queen is associated with a drop in his revenue. Test Bobís suspicion at the 1% significance level. Show all your steps.
ii.[5 marks] Bob claimed that the presence of Burger Queen a§ects the relationship between Hungry Bobís revenue and customer satisfaction score. Test Bobís claim at the 1% significance level. Show all your steps.

2.[Total: 20 marks] Baobao ran the following simple linear regression of y on x Econometrics代考
y = β0+ β1x + u:
He obtained the following summary statistics from the sampled data:
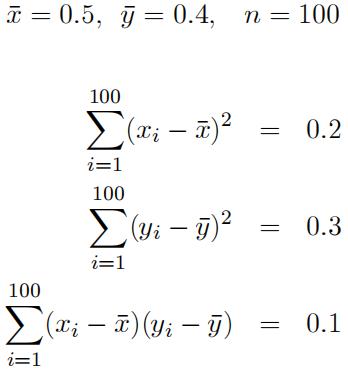
(a) Compute:
i.[3 marks] (OLS estimator of β1 )
ii.[3 marks] (OLS estimator of β0 )
iii. [3 marks] regression R2
iv.[3 marks] SSR (sum of squared residuals)
v.[3 marks] standard error of
(b) [4 marks] Suppose the error series is negatively serially correlated. Will the serial correlation of the error series result in a biased OLS estimator for β1 ? Explain.
3.[Total: 20 marks] Carol is studying the relationship between the number of cars (ncar) and the air quality index (AQI) across a number of countries. She considers the following regression: Econometrics代考
AQI = β0 + β1 ncar + β2 (ncar)2 + u, (1)
She also ran the following auxiliary regression
= γ0 + γ1ncar + γ2 (ncar)2 + v, (2)
where is the residual from regression (1).
The following information was extracted from the ANOVA table associated with the aux-iliary regression :

(a) [6 marks] With the help of the auxiliary regression (2), conduct a test for het-eroskedastic errors in regression at the 5% significance level. Show all your steps.
(b) [4 marks] Suppose the errors in regression (1) are heteroskedastic. Comment on the accuracy of the OLS estimates of β0 , β1 and β2 and their OLS standard errors.
(c) Carol thought that it is reasonable to assume that V ar(ujncar) = σ2 × (ncar)2 for the errors in regression (1).
i.[6 marks] Explain how Carol can transform regression (1) so that the regression errors become homoskedastic.
ii.[4 marks] Describe an alternative method which Carol may use to conduct valid statistical inference on the parameters in regression (1).
更多代写:代做Assignment 托福保分是什么 代上网课价格 代写Essay英文 代写申请文书 生物学网课代修
合作平台:essay代写 论文代写 写手招聘 英国留学生代写