ECON7070, 2021
Practice Questions For Test 4
ECO经济学代考 Firm 1 knows whether it is Strong or Weak. Firm 2 only knows that Firm 1 is Strong with probability 1/3 and is Weak with probability 2/3.
For Questions 1-3, consider the following game.
The players are two fifirms competing in a market. Firm 1 could be in a strong or a weak fifinancial position. Firm 1 knows whether it is Strong or Weak. Firm 2 only knows that Firm 1 is Strong with probability 1/3 and is Weak with probability 2/3. Both fifirms can choose either high, H, or low, L, prices. The payoffffs are as follows:
1.The ex-ante normal form associated with this Bayesian game is:

2.The following is a Bayesian-Nash equilibrium of this game:
(A) Player 1 puts probability 1/2 each on HH and HL and probability 0 on LH and LL: Player 2 plays H with probability 1/2 and L with probability 1/2.
(B) Player 1 puts probability 0 on HH and HL, probability 1/3 on LH and probability 2/3 on LL; Player 2 plays H with probability 1/3 and L with probability 2/3.
(C) Player 1 puts probability 0 on HH and HL, probability 1/2 each on LH and LL; Player 2 plays H with probability 1/2 and L with probability 1/2.
(D) Player 1 puts probability 0 on HH and HL, probability 1/2 each on LH and LL; Player 2 plays H with probability 1/3 and L with probability 2/3.
How to Answer Question 2
- The ex-ante normal form is given in answer A of Question 1.
- Checking for best responses indicates that there is no pure strategy Bayesian-Nash equilib-rium.
- Consider mixed strategy Bayesian-Nash equilibrium
(A) Player 1 puts probability 1/2 each on HH and HL and probability 0 on LH and LL: Player 2 plays H with probability 1/2 and L with probability 1/2.
This cannot be an equilibrium because L gives 0 to player 2 and H gives 1 when player 1 puts probability 1/2 each on HH and HL. Hence player 2 is not indifffferent as he should be in a mixed equilibrium. ECO经济学代考
(B) Player 1 puts probability 0 on HH and HL, probability 1/3 on LH and probability 2/3 on LL;Player 2 plays H with probability 1/3 and L with probability 2/3.
This cannot be an equilibrium because L gives 0 to player 2 and H gives 1 when player 1 puts probability 1/3 on LH and 2/3 on LL. Hence player 2 is not indifffferent as he should be in a mixed equilibrium.
(C) Player 1 puts probability 0 on HH and HL, probability 1/2 each on LH and LL; Player 2 plays H with probability 1/2 and L with probability 1/2.
L and H both give 0 to player 2 when player 1 puts probability 1/2 on LH and LL. However,this cannot be an equilibrium because LH gives 4.5 to player 1 and LL gives 3.5 when Player 2 chooses H and L with probability 1/2. Hence player 1 is not indifffferent as he should be in a mixed equilibrium.
(D) Player 1 puts probability 0 on HH and HL, probability 1/2 each on LH and LL; Player 2 plays H with probability 1/3 and L with probability 2/3. ECO经济学代考
This is a mixed strategy equilibrium. L and H both give 0 to player 2 when player 1 puts probability 1/2 on LH and LL, hence he is indifffferent. LH gives 14/3 to player 1 and LL also gives 14/3 when Player 2 chooses H with probability 1/3 and L with probability 2/3. Hence player 1 is indifffferent as he should be in a mixed equilibrium. Finally, when Player 2 chooses H with probability 1/3 and L with probability 2/3, Player 1 obtains 13/3 form HH and also 13/3 from HL, both are less than 14/3.
3.How much would Firm 2 be willing to pay to discover whether Firm 1 is Weak or Strong? [Hint: With discovery, the outcome is with probability 1/3 the Nash equilibrium of the game when Firm 1 is known to be Strong and with probability 2/3 the Nash equilibrium of the game when Firm 1 is known to be Weak. ]
How to Answer Question 3 ECO经济学代考
- If it is commonly known that Firm 1 is strong, the payoffff matrix is simply the one on the left hand side.
L is a dominant strategy for Player 2 here. Given that player 2 will play L, the best response of player 1 is L. Hence the only Nash equilibrium is (L, L), with a payoffff of 0 for Player 2
- If it is commonly known that Firm 1 is weak, the payoffff matrix is the one on the right hand side.
There is no pure strategy Nash equilibrium. The only Nash equilibrium involves Player 1 playing H with probability 2/3 and L with probability 1/3, while Player 2 plays H with probability 1/3 and L with probability 2/3. Player 2’s equilibrium payoffff is 0.
- Thus if Player 2 knows the state his payoffff is 0, the same as when he knows the state. Hence the amount that Firm 2 is willing to pay is 0. ECO经济学代考
4.There are many sellers of used cars. Each seller has exactly one used car to sell and is characterised by the quality of the used car he wishes to sell.
The quality of a used car is indexed by θ, which is uniformly distributed between 0 and 1. If a seller sells his car of quality θ for price p, his utility is p − θ 2 . If he does not sell his car, his utility is 0. Buyers of used cars receive utility θ − p if they buy a car of quality θ at price p and receive utility 0 if they do not purchase a car. There is asymmetric information regarding the quality of used cars. Sellers know the quality of the car they are selling, but buyers do not know its quality.
Find the highest equilibrium market price p of used cars.
5.Consider a second price auction for a single item with two bidders. Suppose the bidders have independent private values, uniformly drawn in the interval [0, 1]. Suppose the seller sets a reserve price p = 0.5; that is, only bids above p = 0.5 can win. If a bidder bids above p and the other bids below p, then the fifirst bidder wins and pays a price p. If both bid above p, then the highest bidder wins and pays the second highest price.
In the Bayesian equilibrium in undominated strategies, what is the probability that the item will not be sold?
How to Answer Question 5
The item is not sold if both bidders bid below the reserve price p = 0.5. In the Bayesian equilibrium in undominated stratetegies, bidders bid their values. As a result, the probability that the object will not be sold is equal to the probability that both bidders have a value below 0.5.
Given that the value distribution is the uniform distribution for both bidders, the probability that one bidder has a value below 0.5 is 0.5. Hence the probability that both have a value below 0.5 is 0.5 · 0.5 = 0.25. ECO经济学代考
6.Consider a second price auction for a single item with two bidders. Suppose the bidders have independent private values, uniformly drawn in the interval [0, 1]. Suppose the seller sets a reserve price p = 2/5; that is, only bids above p = 2/5 can win. If a bidder bids above p and the other bids below p, then the fifirst bidder wins and pays a price p. If both bid above p, then the highest bidder wins and pays the second highest price.
In the Bayesian equilibrium in undominated strategies, what is the seller’s expected revenue?
How to Answer Question 6
In the Bayesian equilibrium in undominated stratetegies, bidders bid their values. There are three possible sets of events. First, both bidder could have a value below 0.4 = , in which case revenue is zero.
Second, one bidder could have a value below and the other a value above 0.4, in which case the revenue is 0.4, the reserve price. The probability of this second set of events is equal to the sum of two probabilities. The fifirst is the probability that bidder A has a value below 0.4, which is 0.4, times the probability bidder B has a value above 0.4, which is 0.6; that is, 0.4 · 0.6 = 0.24. The second is the probability that bidder A has a value above 0.4, times the probability bidder B has a value below 0.4; this is also 0.24. Hence, the probability that revenue is 0.4 is 0.48.
Third, both bidders could have a value above 0.4, which happens with probability 0.6·0.6 = 0.36.
The price in this set of events is the lowest value of the two bidders having values uniformly distributed in [0.4, 1]. Order statistics of uniform distributions are equally spaced, and hence the expected value of the lowest draw among two values in [0.4, 1] is 0.4 +0.6 = 0.6.
To conclude, revenue is 0.4 with probability 0.48 and on average 0.6 with probability 0.36.Hence, expected revenue is 0.4 · 0.48 + 0.6 · 0.36 = 0.408.
7.Consider a second price auction for a single item with two bidders. Suppose bidder 1 has value uniformly drawn in the interval [0, 1], while bidder 2 has value 0.5
In the Bayesian equilibrium in undominated strategies, what is the seller’s expected revenue?
How to Answer Question 7

In the Bayesian equilibrium in undominated stratetegies, bidders bid their values. There are two possible events.
First, bidder 1 has a value below 0.5 and thus bidder 2 wins. The probability of this event is 0.5 and if this event occurs the price is on average 0.25 (this is on average the value of bidder 1 conditional on the value being below 0.5).
Second, bidder 1 has a value above 0.5 and thus wins the auction. The probability of this event is 0.5 and if this event occurs the price is 0.5 (the value of bidder 2).
Hence the seller’s expected revenue is 0.5 · 0.25 + 0.5 · 0.5 = 0.375. ECO经济学代考
8.Consider a fifirst-price auction for a single item with 2 bidders. Suppose the bidders have inde-pendent private values, uniformly drawn in the interval [0, 1]. Bidders submit bids and the highest bidder wins the item. Which of the following statements is true?
A Each bidder i bids 1/3 of his own value vi .
B Each bidder i bids his own value vi
C Each bidder i bids 1/2 of his own value vi .
D Each bidder i bids 2/3 of his own value vi
9.Which of the statements below is false for the following three-player, extensive form game with imperfect information:
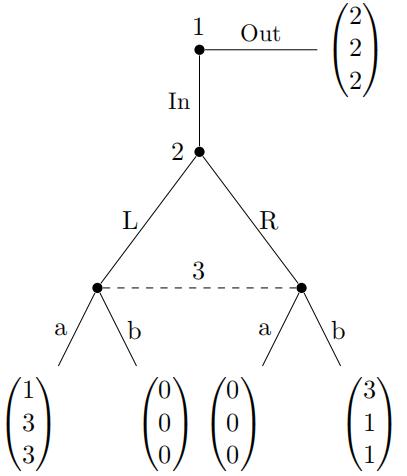
(A) There are two pure strategy subgame perfect equilibria
(B) There is a mixed strategy subgame perfect equilibrium in which Player 2 randomizes between L and R
(C) There is a subgame perfect equilibrium in which the payoffff of Player 1 is 3
(D) There is a subgame perfect equilibrium in which the payoffff of Player 1 is 1
10.Consider the following two-player extensive form game with imperfect information:
For what values of p would player 1 choose R in a subgame perfect equilibrium?
For Questions 11-13, consider the following game.
Two rival fifirms — Firm 1 (Player 1) and Firm 2 (Player 2) are deciding simultaneously on the location to launch their latest products. Each of them can choose to launch their product in either the Red State (action R) or the Blue State (action B). A new initiative of boosting the economy in the Red State may take place, which will change the payoffffs to the fifirms. Firm 2 only knows that there is a probability of 1/2 that the initiative will be carried out. Firm 1, on the other hand,has insider information and knows exactly whether there will be an initiative. The payoffffs are as follows:

11.The ex-ante normal form associated with this Bayesian game is:

12.Which of the following statements is false?
(A) (BR, R) is a Bayesian-Nash equilibrium of this game
(B) (RB, R) is a Bayesian-Nash equilibrium of this game
(C) There is a Bayesian-Nash equilibrium of this game in which Player 2 randomizes between R and B (i.e., puts positive probability on both)
(D) There is no Bayesian-Nash equilibrium in which Player 1 chooses BB with positive probability.
13.How much would Firm 2 be willing to pay to discover whether there is or there isn’t an initiative in the Red state? [ Hint: With discovery, the outcome is with probability 1/2 the Nash equilibrium of the game when Firm 1 is known to be Strong and with probability 1/2 the Nash equilibrium of the game when Firm 1 is known to be Weak. ] ECO经济学代考
14.There are many sellers of used cars. Each seller has exactly one used car to sell and is characterised by the quality of the used car he wishes to sell. The quality of a used car is indexed by θ, which is uniformly distributed between 0 and 1. If a seller sells his car of quality θ for price p, his utility is p − . If he does not sell his car, his utility is 0. Buyers of used cars receive utility θ − p if they buy a car of quality θ at price p and receive utility 0 if they do not purchase a car. There is asymmetric information regarding the quality of used cars. Sellers know the quality of the car they are selling, but buyers do not know its quality. ECO经济学代考
Find the highest equilibrium market price p of used cars.
15.Consider a fifirst price auction for a single item with two bidders. Suppose the bidders have independent private values, uniformly drawn in the interval [0, 1]. Suppose the seller sets a reserve price p = 0.4; that is, only bids above p = 0.4 can win. If a bidder bids above p and the other bids below p, then the fifirst bidder wins and pays a price p. If both bid above p, then the highest bidder wins and pays the second highest price.
In the Bayesian equilibrium in undominated strategies, what is the probability that the item will be sold at price p = 0.4?
16.Consider a second price auction for a single item with two bidders. Suppose the bidders have independent private values, uniformly drawn in the interval [0, 1]. Suppose the seller sets a reserve price p = 1/10; that is, only bids above p = 1/10 can win. If a bidder bids above p and the other bids below p, then the fifirst bidder wins and pays a price p. If both bid above p, then the highest bidder wins and pays the second highest price.
In the Bayesian equilibrium in undominated strategies, what is the seller’s expected revenue?
17.Consider a second price auction for a single item with two bidders. Suppose bidder 1 has value uniformly drawn in the interval [0, 1], while bidder 2 has value 0.4 ECO经济学代考
In the Bayesian equilibrium in undominated strategies, what is the seller’s expected revenue?
18.Consider a fifirst-price auction for a single item with 3 bidders. Suppose the bidders have inde-pendent private values, uniformly drawn in the interval [0, 1]. Bidders submit bids and the highest bidder wins the item. Which of the following statements is true?
A Each bidder i bids 3/4 of his own value vi .
B Each bidder i bids his own value vi
C Each bidder i bids 1/2 of his own value vi .
D Each bidder i bids 2/3 of his own value vi
19.Which of the statements below is true for the following three-player, extensive form game with imperfect information:
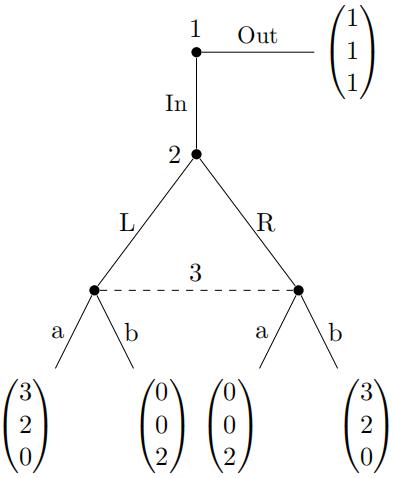
(A) There are two pure strategy subgame perfect equilibria
(B) There is a mixed strategy subgame perfect equilibrium in which Player 1 randomizes between
In and Out
(C) There is a subgame perfect equilibrium in which the payoffff of Player 2 is 1
(D) There is a subgame perfect equilibrium in which the payoffff of Player 1 is 1
20.Consider the following two-player extensive form game with imperfect information:
For what values of p would player 1 choose R in a subgame perfect equilibrium?
更多代写:教育学网课代上 雅思代考价格 加拿大大学课业代写 Essay代写大纲怎么写 education教育学范文 留学生考试代考
合作平台:essay代写 论文代写 写手招聘 英国留学生代写






