DEPARTMENT OF LOGISTICS AND MARITIME STUDIES
Business Management代写 A firm that produces wood shutters and bookcases has received two orders for shutters: one for 180 shutters and one for 135 shutters.
Assignment Business Management代写
Programme: MSc in Business Management
Programme Code : 02012
Session: 2023/24 Semester 1
Subject Code: LGT5171
Subject Title: Contemporary Issues in Operations Management
Date: 10 Nov 2023
Subject Examiner : Prof. Hans Wang
Time: 11:59am 10 Nov−11:59am 17 Nov
Time allowed: 7 days
This question paper has a total of 10 pages (including this covering page). Business Management代写
Instructions to Candidates:
You should write down your answers in this file, or in a separate file, or on a piece of paper and then take a photo of/scan the paper.
The file name of your submission should be “FAMILYNAME Firstname StudentID”, e.g., “TIAN Xuecheng 22047689R.pdf”.
If you encounter problems in submitting your solution, please email your submission to the subject lecturer.
Question 1 (3 marks) Business Management代写
SHARP Electronics Inc. is planning the production for its curved-screen TV for the upcoming four months. Cost data are as follows:
Projected capacity and demand (in units) for curved-screen TVs over the next four months are detailed in the table below (“capacity” means maximum output):
Assume that SHARP currently has 200 units of the TV in inventory.
a) Devise a production plan that aims to end each month with zero inventory while also minimizing the total costs associated with overtime production and subcontracting. Note that backorders are not permitted. Fill in the provided Aggregate Plan template for Question 1a.
Aggregate Plan for Question 1a.
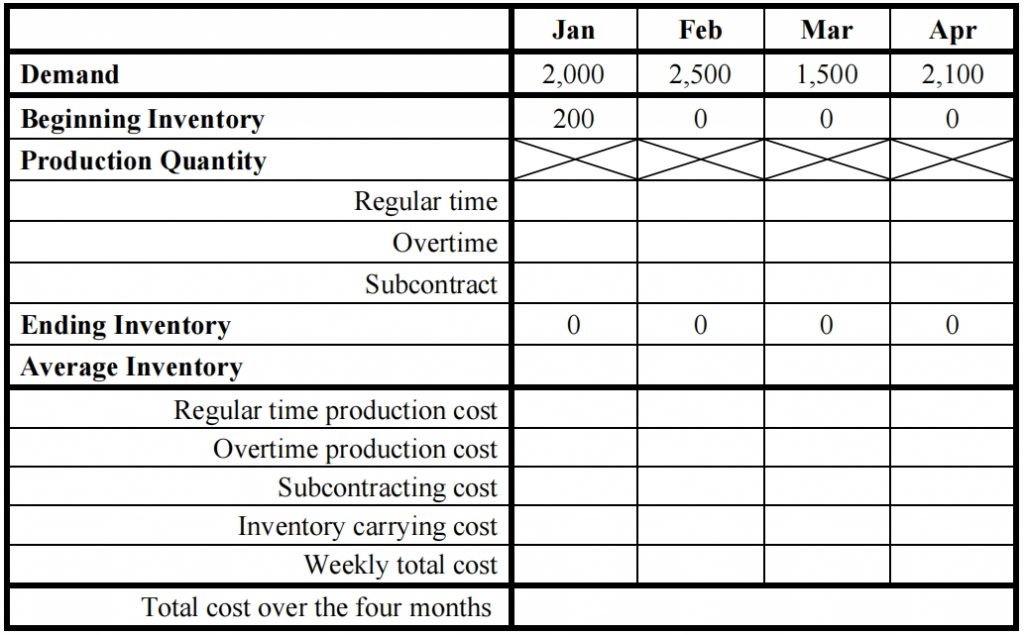
b) Refer to the alternative Aggregate Plan provided for Question 1b. Complete the blanks.Then, determine which plan, 1a or 1b, is more cost-effective by comparing their total costs.
Aggregate Plan for Question 1b.
Question 2 (3 marks) Business Management代写
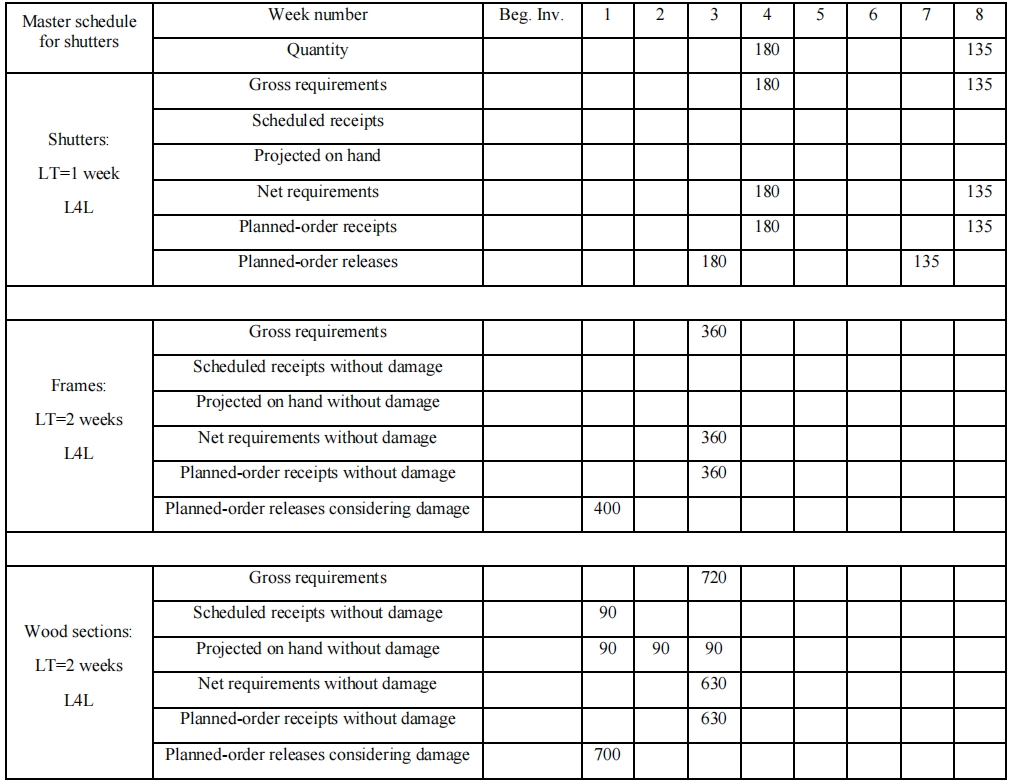
A firm that produces wood shutters and bookcases has received two orders for shutters: one for 180 shutters and one for 135 shutters. The 180-unit order is due for delivery at the start of week 4 of the current schedule, and the 135-unit order is due for delivery at the start of week 8. Each shutter consists of two frames and four slatted wood sections. The firm manufactures the slatted wood sections in-house, requiring two weeks for fabrication. The wood sections have a damage rate of 10% during manufacturing, meaning that the firm must account for this by preparing additional resources.
For instance, to produce 95 sections, the firm must plan for 100 sections to compensate for potential damage. The frames are procured from a supplier with a lead time of two weeks and have a damage rate of 10% during delivery. Similar to the wood sections, the firm must account for this when deciding the number of frames to order. The assembly of the shutters takes one week. There is a scheduled receipt of 90 wood sections without damage in (i.e., at the beginning of) week 1.
a) Your task is to determine the size and timing of the planned order releases that will satisfy the delivery schedules of both orders. You must take into consideration the damage rates for both wood sections and frames. Use the lot-for-lot (L4L) ordering method. Fill in the provided MRP (Material Requirements Planning) Table 2a with this information in appropriate blanks. If the number in a blank is 0, then you do not need toinput the number.
MRP (Material Requirements Planning) Table 2a.
b) Now, consider a new situation: At the beginning of week 2, the firm receives an additional order for 117 shutters, with a delivery deadline at the beginning of week 9.
You are to assume that you are at the beginning of week 2, and you must update the MRP accordingly in Table 2b to reflect this new order. Fill in the provided MRP Table 2b with this information in appropriate blanks (see next page). If the number in a blank is 0, then you do not need to input the number. (Note: the “Planned-order receipts without damage” in week 3 will become “Scheduled receipts without damage” because the order was placed in week 1.)
MRP (Material Requirements Planning) Table 2b.
Question 3 (2 marks)
Daily use of cash register tape averages 10 rolls in a supermarket. Usage appears normally distributed with a standard deviation of 2 rolls per day. The cost of ordering tape per order is $1, and holding cost are $0.001 per roll a day. Lead time is three days. The number of tape rolls to order must be an integer.
a) Determine the optimal quantity of tape rolls the supermarket should order each time to minimize the sum of ordering and holding costs. Show all steps of your calculation process. (Round the solution to the nearest integer. For example, if the optimal fractional quantity is 7.49, then round it to 7.)
b) To maintain stock and avoid shortages during the lead time, the Regional Supermarket must calculate a reorder point (ROP). With a desired lead time service level of 96%,what should the ROP be for the cash register tape rolls? Show all steps of your calculation process. (Round your final answer to the nearest integer number. For example, if the optimal fractional quantity is 7.49, then round it to 7.) (Note: If X follows a standard normal distribution, then Pr(X<1.75) = 0.96.)

Question 4 (3 marks) Business Management代写
Dave Commerce is a wholesaler specializing in the distribution of industrial IoT sensors.The company is reassessing its inventory policy using the Economic Order Quantity (EOQ) model in light of recent demand and cost data. Assume a normal distribution of demand per week throughout the year, which consists of 52 weeks.
Important details are as follows:
Purchase cost = $20 per unit
Ordering cost = $800 per order
Inventory holding cost per unit per year = 40% of the unit purchase cost
Annual demand = 52,000 units
Weekly demand = Annual demand / 52 weeks
Standard deviation of weekly demand = 100 units per week
Lead time = 2 weeks
(a) With the aim of maintaining a stockout risk of no more than 10% (equivalent to a 90% service level) during the lead time, calculate the following: 1) the safety stock level required, 2) the reorder point (ROP), and 3) the appropriate order quantity according to the EOQ model. Note that the safety stock level, the ROP, and the order quantity must all be integers. Show all steps of your calculation process. (Round the solution to the nearest integer. For example, if the optimal fractional quantity is 7.49, then round it to7.) (Note: If X follows a standard normal distribution, then Pr(X<1.28) = 0.9.)
(b) In the event that the lead time extends to 4 weeks due to unforeseen circumstances such as a pandemic, with the aim of maintaining a stockout risk of no more than 10% during the lead time, calculate the following: 1) the safety stock level required, 2) the reorder point (ROP), and 3) the appropriate order quantity according to the EOQ model. Show all steps of your calculation process. (Round the solution to the nearest integer. Forexample, if the optimal fractional quantity is 7.49, then round it to 7.)
Question 5 (3 marks) Business Management代写
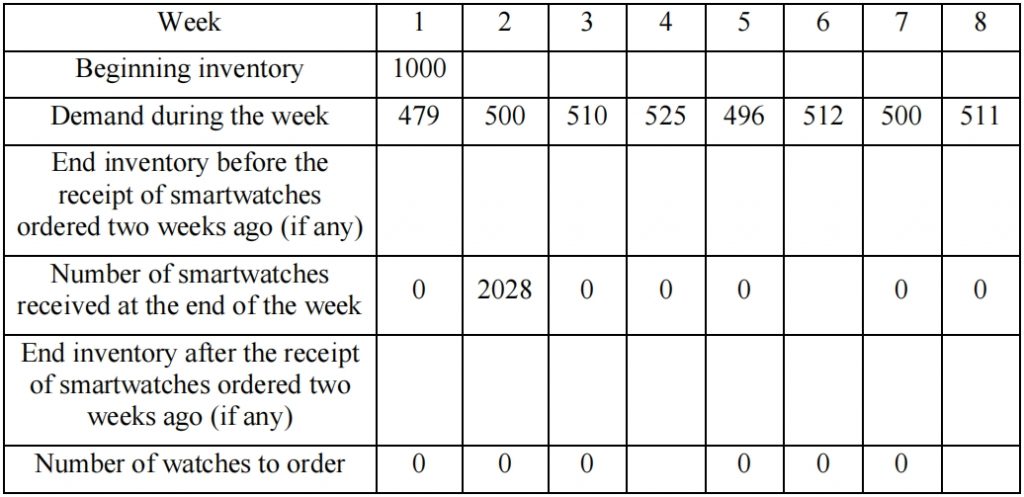
A retail store named “Universal Goods” sells a popular brand of smartwatches. The store has chosen a fixed order interval system for the inventory management of these watches.The weekly demand for these smartwatches follows a normal distribution, with the demand data for the past 8 weeks being: [500, 480, 490, 520, 505, 510, 495, 500] units/week.Universal Goods places an order every 4 weeks (an order is placed at the end of the week every 4 weeks), with a lead time of 2 weeks, and aims for a 95% service level.
Given the demand over the past 8 weeks, we calculate that the mean value of weekly demand is 500 units and standard deviation of weekly demand is 12.25. Using the information provided and considering the store’s service level requirement, complete the blanks in the inventory plan for the next eight months. (Note: If X follows a standard normal distribution, then Pr(X<1.645) = 0.95.) (Round the solution to the nearest integer. For example, if the optimal fractional quantity is 7.49, then round it to 7.)
Inventory Plan Table.
Question 6 (2 marks)
A set of seven jobs needs to be scheduled through two consecutive processes. Each job must first complete Process I before moving to Process II. There are two dedicated machines for these processes: Machine I for Process I and Machine II for Process II. The processing times for each job are as follows:
(a) Apply Johnson’s rule to determine the optimal job sequence for processing through Machines I and II that minimizes the makespan. Present the final sequence of jobs.Calculate the total idle time of Machine II from the start of the schedule to the completion of all jobs. Show all your calculations.
(b) New question: Assume that Job C and Job F are designated as high-priority tasks. These jobs are required to be sequenced before any other tasks are initiated, with Job C commencing prior to Job F. After scheduling the high-priority jobs, the subsequent tasks are to be arranged in accordance with Johnson’s rule to optimize the schedule by minimizing the makespan. Adjust the sequence to schedule the priority jobs first while still attempting to minimize the makespan. Present the final sequence of jobs. Calculate the total idle time of Machine II from the start of the schedule to the completion of all jobs. Show all your calculations.
Question 7 (1.5 marks) Business Management代写
Solve the following problem using software (e.g., Excel, Python, Gurobi, or Cplex) and use screenshots to show the solution process.
⚫ If using Excel, please show the modeling interface, solution settings, and the results.
⚫ If using an optimization solver (e.g., Gurobi or Cplex), please capture screenshots to display the code and the results.
(You can use any software, just make sure to present the process and results clearly. By “solving” a problem, we mean providing the optimal solution to the problem, i.e., the optimal values of the decision variables.)
The minimum weekly staffing requirements of a restaurant are as follows. For example, the number of workers needed on Monday is greater than or equal to 5. Each worker works for 5 days a week and should be scheduled two consecutive days off per cycle. (E.g., Sunday and Monday are considered as two consecutive days off.) We can formulate an integer programming model to determine the minimum number of workers needed.

Decision variables
𝑦––the total number of workers needed;
𝑥1––the number of workers who start working on Monday;
𝑥2––the number of workers who start working on Tuesday;
𝑥3––the number of workers who start working on Wednesday;
𝑥4––the number of workers who start working on Thursday;
𝑥5––the number of workers who start working on Friday;
𝑥6––the number of workers who start working on Saturday;
𝑥7––the number of workers who start working on Sunday.
Question 8 (2.5 marks)
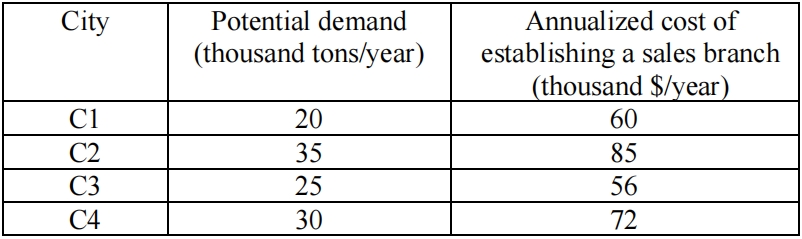
A manufacturer plans to construct a few factories to produce a product P in a region. Three potential factories, denoted as F1, F2, and F3, can be constructed. The manufacturer must construct exactly two factories. The annualized construction cost and capacity of the three potential factories are shown in the following table. The production cost of P is $130/ton and the selling price of P is $200/ton, and the production cost and selling price of P will not be influenced by the production and selling locations.
The region has four cities C1, C2, C3, and C4 that the factories may serve. The potential demand for product P by each city is shown in the following table. Not all demand must be fulfilled. To serve a city (i.e., if a non-zero proportion of the city’s demand is fulfilled), the manufacturer must set up a sales branch in the city. The annualized cost of establishing a sales branch in each city is shown in the following table. The transportation costs of product P from the factories to the cities are 0.
Formulate a mixed-integer programming (MIP) model that can be used to determine which factories to construct, the amount of product P each factory produces, the cities at which sales branches are to be established, and the amount of cargo to transport from each of the factories to each of the cities to maximize the total profit. You can choose one of the following options:
Option 1: Formulate an MIP model from scratch.
Option 2: Complete the following model:
We define notation as follows to simplify the model.
更多代写:加拿大网课代上价格 sat考試作弊 教育学作业代写 英文查重软件 英语论文怎么写 数字媒体代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写








