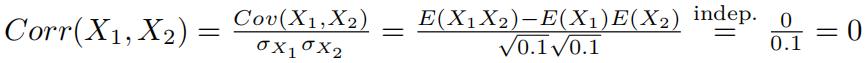APPM 4570/5570
Homework #3
STAT 4000/5000
Assignment统计学代写 Where the cdf of Z can be calculated in R with pnorm( 0.7) and pnorm(3.5) or by simply using the standard normal table.
Problem 1
Note that for the system to work, all of the following have to be satisfied:
–Component 1 has to work
–Atleast one of the components 2, 3, and 4 has to work.
–Atleast one of the components 5 and 6 has to work.
Component 1 has an exponentially distributed lifetime with a mean of 1/2 year. Components 2, 3, and 4 each have an exponentially distributed lifetime with mean lifetime of 1 year. Components 5 and 6 have exponentially distributed lifetimes with mean lifetime of 1.5 year.
Let Xi = the lifetime of component i. Assignment统计学代写
Then, because λ = 1/µ :
X1 Exp(1/0.5) = Exp(2)
fX1 (x) = 2e−2x
FX1 (x) = 1 − e−2x
X2, X3, X4 Exp(1/1) = Exp(1)
fX (x) = e−x
FX (x) = 1 − e−x , for i=2,3,4
X5, X6 Exp(1/1.5) = Exp(2/3)
fX (x) = (2/3)e−2x/3
FX (x) = 1 − e−2x/3 , for i = 5, 6
• a. What is the probability that the system will function uninterruptedly for at least 2 years?
P (F unction at least two years) = P (X1 ≥ 2) ∗ P (X2 ≥ 2 ∪ X3 ≥ 2 ∪ X4 ≥ 2) ∗ P (X5 ≥ 2 ∪ X6 ≥ 2)
P (X1 ≥ 2) = 1 − P (X1 < 2) = 1 − FX1 (2) = 1 − (1 − e−2∗(2)) = e−4
P (X2 ≥ 2 ∪ X3 ≥ 2 ∪ X4 ≥ 2) = 1 − P (X2 < 2 ∩ X3 < 2 ∩ X4 < 2) i.=i.d. 1 − (P (X2) < 2)3
= 1 − (FX2 (2))3 = 1 − (1 − e−(2))3 = 1 − (1 − e−2)3
P (X5 ≥ 2 ∪ X6 ≥ 2) = 1 − P (X5 < 2 ∩ X6 < 2) i.=i.d. 1 − (P (X5 < 2))2 =
1 − (F 1 − (1 − e−2∗(2)/3)2
= 1 − (1 − e−4/3)2
P (F unction at least two years) = (e−4) ∗ (1 − (1 − e−2)3) ∗ (1 − (1 − e−4/3)2) = 0.00296
• b. What is the probability that the system will fail in the ftrst 3 months of the 2nd year.
– We want the probability that the system works for 1 year but fails before 1.25 years Which we can write as:
P(system functions more than 1 year)-P(system functions more than 1.25 years)
P (X1 ≥ 1) ∗ P (X2 ≥ 1 ∪ X3 ≥ 1 ∪ X4 ≥ 1) ∗ P (X5 ≥ 1 ∪ X6 ≥ 1)−
P (X1 ≥ 1.25) ∗ P (X2 ≥ 1.25 ∪ X3 ≥ 1.25 ∪ X4 ≥ 1.25) ∗ P (X5 ≥ 1.25 ∪ X6 ≥ 1.25) Assignment统计学代写
Using techniques from part (a),
= (1 − P (X1) < 1) ∗ (1 − P (X2 < 1)3) ∗ (1 − P (X5 < 1)2)−
(1 − P (X1 < (1.25)) ∗ (1 − P (X2 < 1.25)3) ∗ (1 − P (X5 < 1.25)2)
= [(1 − FX1 (1)) ∗ (1 − FX2 (1)3) ∗ (1 − FX5 (1)2)] − [(1 − FX1 (1.25)) ∗ (1 − FX2 (1.25)3) ∗ (1 − FX5 (1.25)2)]
= [(e−2(1)) ∗ (1 − (1 − e−(1))3) ∗ (1 − (1 − e−2(1)/3)2)]−
[(e−2(1.25)) ∗ (1 − (1 − e−(1.25))3) ∗ (1 − (1 − e−2(1.25)/3)2)] = 0.0416
Problem 2 Assignment统计学代写
Let X be a normally distributed random variable with mean 3 and variance 4.
• a. Let Y = 5X+2. What is the distribution of Y? What are its mean and variance?
Y is normal as it is a linear function of a normal random variable, with mean:
µy = E(Y ) = E(5X + 2) = E(5X) + E(2) = 5E(X) + 2 = 5 ∗ (3) + 2 = 17
and variance:
σ2 = V ar(Y ) = V ar(5X + 2) = V ar(5X) + V ar(2) = 52V ar(X) + 0 = 25 ∗ (4) + 0 = 100
Thus, Y ∼ N ormal(17, 100)
• b. Find P(Y<10). Find P(X<10).
Using the standard normal transformation: Assignment统计学代写
P (Y < 10) = P (Z < (10 − µy)/σy) = P (Z < (10 − 17)/10) = P (Z < −0.7) = Φ(−0.7) = 0.242
P (X < 10) = P (Z < (10 − µx)/σx) = P (Z < (10 − 3)/2) = P (Z < 3.5) = Φ(3.5) = 0.9998
Where the cdf of Z can be calculated in R with pnorm( 0.7) and pnorm(3.5) or by simply using the standard normal table.
• c. What is the 99th percentile of the distribution of Y?
Find y∗ such that P (Y < y∗) = 0.99
Using R, z∗ such that P (Z < z∗) = 0.99 is found by z∗ = qnorm(0.99) = 2.326 And, z = (y − µy)/σy
So, y∗ = z∗ ∗ σy + µy = (2.326) ∗ (10) + (17) = 40.26
• d. What is the 99th percentile of the distribution of X?
Similarly, still dealing with the 99th percentile, i.e. z∗ = 2.326 Assignment统计学代写
x∗ = z∗ ∗ σx + µx = (2.326) ∗ (2) + (3) = 7.65
• e. What is the distribution of W = exp(Y)? What are its mean and variance?
W = exp(Y ) is log-normal because log(W ) = Y is normally distributed. Thus,
µW = E(W ) = exp{µy + σ2/2} = exp{17 + 100/2} = exp{67} = e67 = 1.252 ∗ 1029
σ2 = V ar(W ) = exp{2µy +σ2}∗(exp{σ2}−1) = exp{2(17)+(100)}∗(exp{(100)}−1) = e134 ∗(e100 −1)
= 4.22 ∗ 10
W ∼ LogN ormal(17, 100)

Problem 3 Assignment统计学代写
Let X1, X2, X3, X4, X5 and X6 denote the numbers of blue, brown, green, orange, red, and yellow M&M candies, respectively, in a sample of size n. According to the M&M Web site, the color proportions are p1=0.24, p2=0.13, p3=0.16, p4 = 0.20, p5 =0.13, and p6 =0.14.
• a. If n = 12, what is the probability that there are exactly two M&Ms of each color?
Use multinomial distribution:
P (X1 = 2, X2 = 2, …, X6 = 2) = 12! ∗(0.242)∗(0.132)∗(0.162)∗(0.202)∗(0.132)∗(0.142) = 0.00247
• b. For n = 20, what is the probability that there are at most ftve orange candies? (Hint: Treat an orange candy as a success and any other color as a failure)
Let X= number of orange selected
From the hint, consider a binomial distribution with p = p4 = 0.2 Assignment统计学代写
i.e. X ∼ Bin(20, 0.2)
Then, P (X ≤ 5) = Σ5 .20Σ(p)x(1 − p)20−x = Σ5 .20Σ(0.2)x(0.8)20−x = 0.804
• c. In a sample of 20 M&Ms, what is the probability that the total number of candies that are blue, green, or orange is at least 10?
Let X= number of blue, green, or orange selected
Now consider a binomial distribution with p = p1 + p3 + p4 = 0.6
i.e. X ∼ Bin(20, 0.6)
This can be done in R with the following code: 1 − pbinom(9, 20, 0.6) = 0.8724788
This can also be calculated as a multinomial distribution using the following code in R:
p1=0
for (i in 0:9) {
for (j in 0:(9-i)) {
for (k in 0:(9-j-i)) {
for (l in (20-i-j-k):(20-i-j-k)) {
p1 = c(p1,dmultinom(x=c(i,j,k,l),prob=c(.24,.16,.2,.4)))
}}}}
Answer=1-p1= 0.8724788
Problem 4
Please answer and provide a brief justification of your answer:
• a. Can covariance between two random variables be less than -1?
Yes, covariance between two random variables can be much less than -1, as covariance is not normalized, however correlation cannot be less than -1, as it is normalized.
• b. If covariance between two random variables is negative, does their correlation have to be negative?
Yes, if covariance is negative, correlation has to be negative. This is because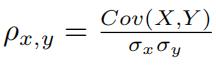
• c. If correlation between two random variables is negative, does their covariance have to be negative?
Yes, if correlation between two random variables is negative, their covariance must be negative.
Cov(X, Y ) = ρx,y ∗ σx ∗ σy so the covariance must have the same sign as the correlation.
• d. Can correlation between two random variables be bigger than 1?
No, −1 ≤ ρx,y ≤ 1. The magnitude of correlation cannot exceed 1. Assignment统计学代写
• e. If Cov(X,Y)= 0.3, what is Cov(100X,Y)?
Cov(100X, Y ) = 100 ∗ Cov(X, Y ) = 100 ∗ (0.3) = 30
• f. If Corr(X,Y) = 0.1, what is Cov(100X,Y)?
Cov(100X, Y ) = Corr(100X, Y ) ∗ σ100X ∗ σY = sgn(100 ∗ 1) ∗ Corr(X, Y ) ∗ 100σX ∗ σY = 1 ∗ 0.1 ∗ 100σX ∗ σY = 10σXσY
• g. What is Cov(X,X)?
Cov(X, X) = E(XX) − E(X)E(X) = E(X2) − (E(X))2 = V ar(X)
• h. What is Corr(X,X)?
• k. What is Cov(100X,10X)?
Cov(100X, 10X) = 100 ∗ 10 ∗ Cov(X, X) = 1000 ∗ V ar(X)
• l. What is Corr(100X,10X)?
Corr(100X, 10X) = sgn(100 ∗ 10) ∗ Corr(X, X) = 1 ∗ 1 = 1
Problem 5 Assignment统计学代写
A rock specimen is randomly selected and weighed two different times. Let w denote the true weight (a number) of the rock, and let X1 and X2 be the two measured weights. Then, X1 = w + E1, and X2 = w + E2, where E1 and E2 are the two measurement errors. Suppose that E1 and E2 are independent, and distributed normally with mean 0 and variance equal to 0.1 (ie, E1, E2 ∼ N (0, 0.1)).
• a. What is the mean of X1? What is the mean of X2?
µX1 = E(X1) = E(w + E1) = E(w) + E(E1) = w + 0 = w
µX2 = E(X2) = E(w + E2) = E(w) + E(E2) = w + 0 = w
• b. What is Var(X1)? What is Var(X2)?
V ar(X1) = V ar(w + E1) = V ar(w) + V ar(E1) = 0 + 0.1 = 0.1
V ar(X2) = V ar(w + E2) = V ar(w) + V ar(E2) = 0 + 0.1 = 0.1
• c. What is Corr(X1,X2)?
更多代写:AI代写 Gmat代考 英国网课作业代写范例 Critical Review Essay代写 biotechnology论文代写 网课托管平台价格