Practice Test Questions
量化模型代考 A chemical company must produce exactly 1,000 kilograms of a special mixture of phosphate and potassium for a customer.
Question 1
A publishing company is planning on developing an SPSS Manual for graduate students in doctoral programs. The book will cost $16 to produce and will sell for $24; fixed costs will be $160,000. The company estimates that sales will be approximately 60,000.
a)What is the company’s breakevenpoint?
b)Find the estimated profit.
Question 2 (6 marks)
A chemical company must produce exactly 1,000 kilograms of a special mixture of phosphate and potassium for a customer. The phosphate costs $5 per kilogram and potassium costs $6 per kilogram. No more than 300 kilograms of phosphate can be used, and at least 150 kilograms of potassium must be used. The problem is to determine the least-cost blend of the two ingredients. Restate the problem mathematically by:
a)Showing the decisionvariables
b)Showing the objectivefunction
c)Showing theconstraints
d)Solve the linear programming problem bygraphing
Question 3 量化模型代考
A production process can make either 3 units per hour of product A or two units per hour of product B. If X(A) equals the number of units of A and X(B) equals the number of units of B to produce, and there are only eight hours of production time available, show how the constraint can best be expressed as a linear inequality.
Question 4
A feasible solution:
a)May violate only oneconstraint
b)Can only be determined using acomputer
c)Satisfies all theconstraints
d)May not be on the boundary of a feasiblearea
Question 5 (1 mark)
A linear programming problem is subject to six constraints. Rewrite the following constraint in the approved format: x1 ≤ 2×2

Question 6 量化模型代考
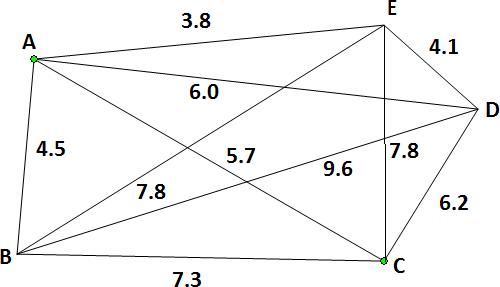
The following table shows the distances in km between 16 locally incorporated banks in Melbourne. The arcs are not directed (they permit to travel in either direction).
Draw the network and use the shortest route algorithm to find the shortest distance from node 1 (office from which deliveries are made) to each bank.
| Branch | Distance(km) | Branch | Distance(km) |
| 1-2 | 23 | 7-10 | 19 |
| 1-3 | 17 | 7-11 | 21 |
| 1-4 | 20 | 8-12 | 22 |
| 2-5 | 12 | 9-13 | 17 |
| 2-6 | 13 | 10-13 | 18 |
| 3-7 | 13 | 11-12 | 13 |
| 4-8 | 15 | 11-14 | 15 |
| 5-6 | 10 | 12-15 | 110 |
| 5-9 | 18 | 13-14 | 12 |
| 6-7 | 12 | 13-16 | 20 |
| 6-9 | 11 | 14-16 | 16 |
| 7-8 | 24 | 15-16 | 27 |
Question 7
The cost of connecting electrical wires from five outback towns in Western Australia is represented in the network below. Highlight the arcs of the minimal spanning tree and show the length in the correct unit of measurement.
Cost in $100,000
Question 8 量化模型代考
Given the following network, with the indicated one-way flow capacities (in hundreds of litres of water) along each branch, determine the maximum flow from the source at node B to the sink at node M. Also fill in the table shown underneath the network.

| Route | Flow | Blocked
Routes |
Flow from
Source |
Flow to
Sink |
Question 9
A furniture company buys two products for resale: big shelves (B) and medium shelves (M). Each big shelf costs $500 and requires 100 cubic feet of storage space, and each medium shelf costs $300 and requires 90 cubic feet of storage space. The company has $750,000 to invest in shelves this week and the warehouse has 180,000 cubic feet available for storage. Profit for each big shelf is $300 and for each medium shelf is $150. What is the storage space constraint?
a) 100(B) + 90(M) ≤ 180,000 b)
90(B) + 100(M) ≥180,000 c)
500(B) + 300(M) ≥ 180,000 d)
500(B) + 300(M) ≤180,000
Question 10 量化模型代考
For there to be three times as many units of A as of B the inequality is written as
a)3A ≥B
b)A ≥3B
c)A ≤3B
d)B ≤3A
Question 11
The production of A must be three and a half times the production of B and C. Show how you would set out the problem
a) A ≥ 5 (B + C)
b)the production of A to B and C is at least 1 to 3.5
c)5A ≥ B + C
d)A ≤(B + C)
更多代写:matlab作业代做 托福代考 英国Midterm代考推荐 Comparative Essay代写 argumentative essay论文代写 为什么要选择网课代上