ECMT5001: In-semester Exam (2022s2)
计量经济学期中代写 Let B and C denote, respectively, the number of buses and construction vehicles crossing the bridge in one minute.
Time allowed: 1.5 hours
The total score of this exam is 40 marks. Attempt all questions. Correct all numerical answers to 2 decimal places.
1.[Total: 15 marks] Bob was studying the traffic fiow on Sydney Harbour Bridge. 计量经济学期中代写
Let B and C denote, respectively, the number of buses and construction vehicles crossing the bridge in one minute. Equipped with his expertise in buses, Bob decided to model B according to the Poisson distribution with mean 4.
(a) [3 marks] What is the probability that more than two buses crossed the bridge in a minute?
(b) [3 marks] Given that more than two buses crossed the bridge in a minute, what is the probability that more than three buses crossed the bridge in a minute?
Upon further observation, Bob decided to model C according to the Poisson distrib-ution with mean 9. He assumed that the correlation between B and C is 0.6.
The toll company charges $5 for each bus and $20 for each construction vehicle cross-ing the bridge. Let R denote the total revenue generated from buses and construction vehicles in a minute.
(c) [2 marks] Compute E(R).
(d) [4 marks] Compute V ar(R) [Hint: it is true that V ar(X) = E(X) if X is Poisson distributed.]
(e) [3 marks] Explain to Bob why a Poisson model is a poor model to use in practice.

2.[Total: 25 marks] Carol has been closely watching the share price of a technology company called Blueberry Inc. 计量经济学期中代写
(with stock code BRRY). Let X denote the change in share price (in number of ticks) in a second (i.e., X = 1 if there is an uptick, = 0 if there is no change, and =-1 if there is a downtick). Based on the historical behaviour of the stock price, Carol modelled X according to the following probability density function:
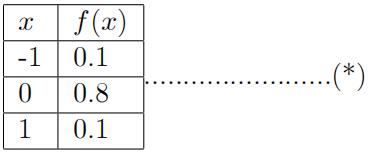
(a) [1 mark] Find E(X).
(b) [2 marks] Compute V ar(X).
(c) [3 marks] Compute Cor(X; X2).
In an attempt to validate her model, Carol computed the mean price changes of BRRY over n randomly chosen one-second intervals. Suppose the price changes X1; X2; : : : ; Xnare iid with the common distribution given by (*). Letdenote the mean price change (in ticks per second).
(d) [2 marks] Using the result of part (a), what is E()? Justify your answer by pointing out a property of
. [Hint: no calculation is needed.]
(e) [2 marks] Using the result of part (b), compute V ar(). 计量经济学期中代写
(f) [5 marks] Obtain the probability density function of  .
.
In light of the symmetry of (*) around zero, Carol claimed that BRRY breaks even on average (i.e., the mean price change is zero).
(g) [6 marks] Based on a given sample of 80 randomly chosen one-second intervals, there was a mean price drop of 0.1 ticks (i.e.,=-0.1).Test at the 5% significance level whether Carolís claim is correct. Show all your steps. A complete response should include:
i.setting up the null and alternative hypotheses;
ii.defining an appropriate test statistic;
iii. stating the distribution of your test statistic under the null hypothesis; 计量经济学期中代写
iv.computing the test statistic based on the sampled data;
v.making a decision using a correct method (e.g., critical value approach or p-value approach); and
vi.drawing a conclusion.
(h) [4 marks] By enlarging her sample in part (g) so that n > 80, Carol still observed a mean price drop of 0.1 ticks. Will your conclusion in part (g) remain valid or not?Explain your answer.
更多代写:化学网课代做 代考价格 会计Final exam代考 加拿大留学生essay代写 教育学毕业论文代写 代考计算机系统组织
合作平台:essay代写 论文代写 写手招聘 英国留学生代写