Computer Science
EXAMINATION
Semester 2 – Practice, 2021
comp2022 Models of Computation
计算模型代考 This is an OPEN book examination. You are allowed to use passive information sources (i.e., existing written materials such as books and websites);
EXAM WRITING TIME: 3 hours
READING TIME: 10 minutes
EXAM CONDITIONS: 计算模型代考
This is an OPEN book examination. You are allowed to use passive information sources (i.e., existing written materials such as books and websites); however, you must not ask other people for answers or post questions on forums; always answer in your own words. You must not reveal the questions to anyone else.
All work must be done individually in accordance with the University’s “Aca-
demic Dishonesty and Plagiarism” policies.
INSTRUCTIONS TO STUDENTS:
- Type your answers in your text editor and submit a single PDF via Canvas; all prose must be typed. Figures/diagrams can be rendered any way you like (hand drawn,latex, etc), as long as they are perfectly readable and part of the submitted PDF.
- Start by typing your student ID at the top of the first page of your submission.Do not type your name.
- Submit only your answers to the questions. Do not copy the questions. Start each of the five problems on a new page.
- If the required level of justification is not stated, you should briefly justify your answer.
For examiner use only:
| Problem | 1 | 2 | 3 | 4 | 5 | Total |
| Marks | ||||||
| Out of | 14 | 10 | 14 | 8 | 4 | 50 |
Problem 1. 计算模型代考
These questions are about Propositional Logic. If the required level of justification is not stated, you should briefly justify your answer.
a)Isit the case that the formulas p →(p→ q) and q→ (q→ p) are logically equivalent?
b)Using the equivalences from the tables provided with the exam, showthat
((p ∨ (q ∨ r)) ∧ (r ∨ ¬p)) ≡ ((q ∧ ¬p) ∨ r)
You may type your answer in a table or as a sequence of lines, or you may draw the table and insert it into your pdf. No marks will be awarded for proofs that do not use the rules taught in this course and summarised in the tables provided with the exam.
c)Prove the following consequent in naturaldeduction:
b → d, d → a, c ├ a ∨ (b → ¬c)
You may type your answer in a table or as a sequence of lines, or you may draw the table and insert it into your pdf. No marks will be awarded for proofs that do not use the rules taught in this course and summarised in the tables provided with the exam. 计算模型代考
d)An undirected graph G = (V, E) is called bipartite if there is a subset X⊆V such that every edge in G has one endpoint in X and the other not in X. Say V ={ 1, 2, , n }. To encode the problem of deciding if a graph is bipartite or not, you introduce variables xi for 1 ≤ i ≤ n. The meaning of xi being true is that i X. Write a formula ΦG in CNF over the variables x1, x2, , xn that expresses that the graph is bipartite, i.e., ΦG is satisfiable if and only if G is bipartite.
e)What is wrong with the following recursive algorithm deciding whether a given propositional formula F in NNF is satisfiable or not:
-
- IfF is an atom or the negation of an atom, return ”Satisfiable”.
- If F= (F1 F2) then check if both F1 and F2 are satisfiable. If they are, then return “Satisfiable”, else return “Unsatisfiable”.
- If F= (F1 F2) then check if either F1 or F2 are satisfiable. If at least one is, then return “Satisfiable”, else return “Unsatisfiable”.

Problem 2. 计算模型代考
These questions are about Context-free Languages. If the required level of justification is not stated, you should briefly justify your answer.
a)Consider the following CFG inCNF:
S → AX | AB | ∈
T → AX | AB
X → TB
A → a
B → b
- Statethe variables and terminals of the grammar.
- Which variables derive the stringaabbb?
- The CYK algorithm computes a 2D-array Table where Table(i, j) are thevariables that derive the substring starting at position i and ending at position j. In order to compute Table(2, 5), which entries of the table are directly needed to be checked/computed?
b)Explain why if L is a regular language then L is generated by an unam- biguous context-free grammar.
c)Write a context-free grammar for the following language: the set of strings of the form u#v where u, v ∈ {a, b}∗ and |u| = |v| and the reverse of u is not equal to v.
Problem 3. 计算模型代考
These questions are about Regular Languages. If the required level of justification is not stated, you should briefly justify your answer.
a)Give a regular expression that recognises the language of all stringsover{a, b}∗ which has neither aa nor bb as a substring.
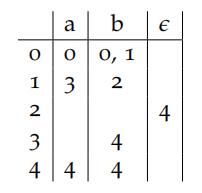
b)Considerthe NFA N = (Q, Σ, δ, q0, F) where Q = {0, 1, 2, 3, 4}, Σ = {a, b},[4 marks]
q0 = 0, F = {4}, and δ is as follows:
If you were to apply the technique you learned in class to convert N into an equivalent DFA D,
- What is the initial stateof D?
- Whatstates of D are reachable from the initial state?
- What states of D are reachable from the intial state and are also ac- cepting states ofD?
No additional explanation is needed. 计算模型代考
c)Your friend tells you there is a regular expression that matches those doc- umentsthat contain mis-matched Explain why your friend is mistaken by defining a language that models “documents with mis- matched parentheses” and proving, using methods taught in the course, that there is no regular expression for it. You may use the fact that the language of balanced parentheses is not regular.
d)Let G = (V, E) be a finite directed-graph, i.e., V is a finite set of vertices and E ⊆ V × V is a set of edges. A path in G is a finite non-empty sequence of vertices v0v1vk such that (vi, vi+1) E for every i with 0 ≤ i < k. Show that the set of paths of G is a regular language over the alphabet V.
e)Consider the operation neg that maps a binary string u ∈ { 0, 1 } ∗ to the string in which every 0 is replaced by 1 and vice versa. So, e.g., neg(0111) = Show that if L ⊆ {0, 1}∗ is regular, then so is {neg(u) : u ∈L}.
Problem 4.
These questions are about Turing Machines. If the required level of justification is not stated, you should briefly justify your answer.
a)Isit the case that every finite language is decidable?
b)Oneof your assignments showed one way of encoding a context-free gram- mar as a single string (if you consider the new-line/carriage-return as a separator). Is the set of encodings of context-free grammars Turing- decidable?
c)Showthat if L is in P and Lj is in NP then L ∩ Lj is in NP.
d)Showthat if L is in P then L∗ is in P.
Problem 5. 计算模型代考
These questions are about Predicate Logic. If the required level of justification is not stated, you should briefly justify your answer.
a)Consider the domain of people, that includes Mick and Sue, and the fol- lowingpredicates:
-
- child(x, y) is a binary predicate saying that person x is a child of persony.
- eq(x, y) is a binary predicate saying that x and y are the same person. Usethis to write the following statements in predicate logic:
- Mickis either the child of Sue, or Sue is the child of Mick.
- Every person is a child.
- x and y have exactly one child together.
- Mick has at least one child with Sue, and no children with anyone else.
No additional explanation is needed.
更多代写:Java代考价格 多邻国代考 数学代写价格 导师推荐信英文 英文论文封面 英文论文范文
合作平台:essay代写 论文代写 写手招聘 英国留学生代写