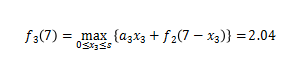4.2件杂货码头装卸作业线效率模型分析
计算机作业辅导 建模的主要目标是对所有作业线的后方机械进行系统性优化,以实现最高的总体效率水平。在建立件杂货码头装卸作业线后方机械配置的数学模型时,有必要对实际情况进行合理的简化处理。具体的假设条件为以下个方面:(1)每一次优化配置之前,已知确定的待作业船的数量为,且每条船装同一种货物,为每一条船···
4.2.1模型的假设 计算机作业辅导
建模的主要目标是对所有作业线的后方机械进行系统性优化,以实现最高的总体效率水平。在建立件杂货码头装卸作业线后方机械配置的数学模型时,有必要对实际情况进行合理的简化处理。具体的假设条件为以下个方面:
(1)每一次优化配置之前,已知确定的待作业船的数量为,且每条船装同一种货物,为每一条船配置上门机、后方机械和其他设备,称作一条作业线;
(2)装卸作业中可供使用的机械设备总数量为已知条件。假设除吊车设备外,其他机械由于单价相对较低,数量十分充足,均可以达到需要。
(3)装卸作业过程中,作业线所采用的装卸工艺及使用门机的数量由生产调度人员选择确定;
(4)配置计划内的作业线不允许出现排队状况,即不允许出现作业线效率为零的情形;
4.2.2模型的建立
以下以吊车作为短缺机械,说明模型的建立。设每条装卸作业线上吊车的相对作业效率为Ai,则:
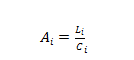
上式中:Li为第条作业线分配的吊车作业效率,Li=XiQi,其中,Xi为第i条作业线配置的吊车数量,Qi为单台吊车作业效率,Ci为第i条作业线分配的门机作业效率
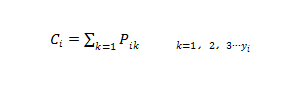
上式中;Pik为第i条作业线上第k台门机的作业效率;yi为第i条作业线配置的门机数量;假设n为待配置作业线总数,实际上
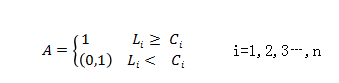
系统优化目标函数可以规划为求解 计算机作业辅导
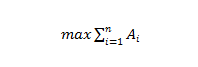
将公式(4-1),(4-22)带入(4-3),得出模型为:
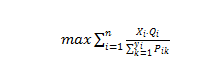
将上述目标函数改写为:
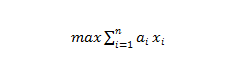

公式中,S max为可调度吊车总台数
4.2.3模型的求解 计算机作业辅导
所建立的优化模型属于整数规划问题,此处选用动态规划算法中的最佳原理法来求解,下面仍然以吊车为短缺设备说明模型的解法。给出具体数据如下:
n=3,Smax=7,a1=0.24,a2=0.32,a3=0.28
最合理的吊车配置问题为;
(4-8)
式中:x1,x2,x3分别为3条船舶A,B,C的吊车配置数:
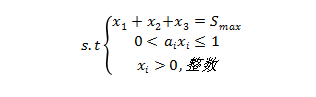
利用最佳原理将其转化为多段判决问题,假设fk(s)为将台吊车配置给前k条船,所得到k条作业线的相对作业效率之和,s为可分配的吊车数。将6台吊车分别配置到3条作业线,其相对作业效率Ai如表1。
表4.1相对作业效率Ai
| 作业线 | 吊车配置数 | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| A | 0.24 | 0.48 | 0.72 | 0.96 | 1 | 1 | 1 |
| B | 0.32 | 0.64 | 0.96 | 1 | 1 | 1 | 1 |
| C | 0.28 | 0.56 | 0.84 | 1 | 1 | 1 | 1 |
以下为具体的求解步骤
(1)仅考虑A船,s与相对作业效率之和的关系如下:
(4-10)
此时,x1=s,s与f1(s)的关系见表2.
表4.2 s与f1(s)的关系
| f | s | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| f1(s) | 0.24 | 0.48 | 0.72 | 0.96 | 1 | 1 | 1 |
(2) 考虑,A,B两船,s与相对作业效率之和f2(s)的关系参见公式(4-8)
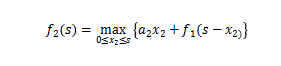
S与f2(s)的关系如表上 所列
表 4.3 s与f2(s)的关系
| s | x2 | f2(s) | |||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||
| 1 | 0.24 | 0.32 | 0.32 | ||||||
| 2 | 0.48 | 0.24+0.32=0.56 | 0.64 | 0.64 | |||||
| 3 | 0.72 | 0.48+0.32=0.80 | 0.24+0.64=0.88 | 0.96 | 0.96 | ||||
| 4 | 0.96 | 0.72+0.32=1.04 | 0.48+0.64=1.12 | 0.24+0.96=1.20 | 1 | 1.2 | |||
| 5 | 1 | 0.96+0.321.28 | 0.72+0.64=1.36 | 0.48+0.96=1.44 | 0.24+1=1.24 | 1 | 1.44 | ||
| 6 | 1 | 1+0.32=1.32 | 0.96+0.64=1.60 | 0.72+0.96=1.68 | 0.48+1=1.48 | 0.24+1=1.24 | 1 | 1.68 | |
| 7 | 1 | 1+0.32=1.32 | 1+0.64=1.64 | 0.96+0.96=1.92 | 0.72+1=1.72 | 0.48+1=1.48 | 0.24+1=1.24 | 1 | 1.92 |
(3)考虑A,B,C 3条船舶,s与相对作业效率之和f3(s)之间的关系如下:
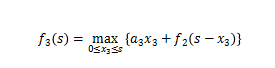
所以:
从表4.4中可以清楚的发现,x1=1; x2=3; x3=3时,目标函数maxA=a1x1+a2x2+a3x3取最大值2.04。此时,A1=0.24; A2=0.96; A3=0.84。
表4.4 求解f3(7) 计算机作业辅导
| x3 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| a3x3 | 0 | 0.28 | 0.56 | 0.84 | 1 | 1 | 1 | 1 |
| f2(7-x3) | 1.92 | 1.68 | 1.44 | 1.2 | 0.96 | 0.64 | 0.32 | 0 |
| a3x3+f2(7-x3) | 1.92 | 1.96 | 2 | 2.04 | 1.96 | 1.64 | 1.32 | 1 |
此方案为最优方案。当确定了x1=1.x2=3,x3=3之后,可以再对门机的配置数量进行校验,以确定门机数量是否是科学、合理的。在上述例子之中,B,C线配备的吊车数为辆,也已实现满负荷作业,门机数量按此前的预定不变,但A线的吊车数量为1辆,门机设备尚没有实现满负荷作业,可以依据a1x1=0.24,适当加以减少。
4.3模型的主要结论
(1)在上述求解过程之中,假定短缺的设备为吊车。实际应用过程中,短缺
设备是依据实际情况推算出来的,仅仅需要将本模型之中的吊车替换为其它机械装置就可以了。因此本文之中模型对码头装卸作业的机械配置具备一定的普适性。
(2)在装卸作业活动之中,当作业情况发生变化时,例如一条船作业完毕,或有新的船舶抵达码头,可以常试性地使用本文中的模型实施再一次的安排和配置。通过对本文模型的灵活使用可以动态优化件杂货码头的后方机械配置,从而实现件杂货码头作业效率的最大化。
更多代写:X86汇编代写 生物学代考 统计学代写 apa论文 lab report怎么写 java辅导