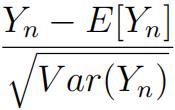Homework 2 Due 5-21 by 10:00 pm EST
英国统计作业代写 Solve the problems in the spaces provided and save as a single PDF. Then upload the PDF to Canvas Assignments by the due date.
Instructions: Solve the problems in the spaces provided and save as a single PDF. Then upload the PDF to Canvas Assignments by the due date. The recommended procedure is to download and print the homework. Fill in your solutions. Then scan the document and upload to Canvas Assignments. If this is not feasible, you may solve the problems on your paper, scan your solutions, then upload to Canvas. Neatness and presentation are important. Late homework not accepted. Show all work.
Total points: 30
1) Let X1, X2, . . . Xn be iid from Exponential(1/θ). That is 英国统计作业代写
x > 0
Calculate E[nX(1)] where X(1) is the smallest order statistic. (2 points)
2) Let X1, X2 be iid N(0, 1). Let
Y1 = g1(X1, X2) = X1 + X2 Y2 = g2(X1, X2) = X1 − X2
a) Find the joint pdf f(y1, y2). Defifine the support of the joint pdf. (3 points)
b) Are Y1 and Y2 independent? (1.5 points)
c) What are the marginal distributions of Y1 and Y2? (1.5 points)
3) Suppose that X and Y are jointly continuous random variables such that X ∼ U(0, 1) 英国统计作业代写
and
fY |X(y|x) = 1 x < y < x + 1.
Find Cov(X, Y ). (3 points)
Hint: You don’t have to, but try the conditional expectation formulas.
4) Let
Suppose V ar(aX − bY + cZ) = 97. Find Cov(Y, Z). (2.5 points)

5) Let Y1, Y2, . . . , Y11 be iid N(µ, σ2 ) so that n = 11. Find 英国统计作业代写
P (0.325 < < 2.048)
Hint: This problem comes from Lecture 6. Tables are in the back of your book.(1.5 points)
6) Suppose Z ∼ N(0, 1) and V ∼ χ 2n are independent. Let
Y = V.
Derive the density of the t-distribution on n degrees of freedom by fifinding 英国统计作业代写
a) The joint density fT,Y (t, y). (2.5 points)
b) The marginal density fT (t) using the result in a). (3 points)
See page 193 Proposition A for the density function of the t distribution. The calculations here are a little tedious, but stay with it and follow through.
7) Suppose X is uniformly distributed on the interval (0, 10). That is, X ∼ U(0, 10). Let
Y = max(4, X) where max is the maximum value. Find E[Y ]. (3 points)
8) Demonstration of the Central Limit Theorem.
Let X1, X2, . . . , Xn variables a sequence of independent and identically distributed random from U(− ,
).Set n = 100.
a) What are E[Xi] and V ar(Xi) for each i = 1, . . . , n? (1 point)
b) Let Yn = X1 + · · + Xn. What are E[Yn] and V ar(Yn) for n = 100? (1 point)
c) According to the Central Limit Theorem, what distribution does 英国统计作业代写
tend to as n → ∞? (1 point)
d) Using the results above, estimate P(−16.5 < Yn< 16.5). (1.5 points)
e) Let = Yn/n. What are E[
] and V ar(
)? (1 point)
f) Using R, generate 100,000 independent
U(− ,
) random variables and put them in a 100× 1000 matrix. Calculate
for each column, giving a sample of size 1,000 from the distribution of
. Calculate the mean and standard deviation of the sample (recall that the standard deviation is the square root of the variance). Are the results compatible with the results found in e)? Make a histogram of the sample drawn from the distribution of
and turn in with the homework. The commands in R are given below: (1 point)

1) Let X and Y be exponential random variables with parameter 1. That is
f(x) = e−x x > 0 f(y) = e−y y > 0
and X and Y are independent. Find the probability density function of the random variable Z = X/(X + Y ). Make sure to defifine the support of Z.
更多代写:北美考试代考 留学代考 北美留学生assignment代写 网课reflection essay代写 新西兰留学生论文代写 美国统计代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写