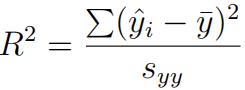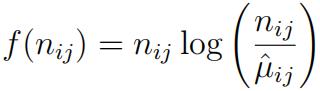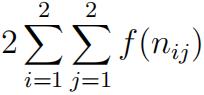Stats 426 Spring 2021
Homework 5 Due 6-18 by 10:00 pm EST
美国统计代写 Solve the problems in the spaces provided and save as a single PDF. Then upload the PDF to Canvas Assignments by the due date.
Instructions: Solve the problems in the spaces provided and save as a single PDF. Then upload the PDF to Canvas Assignments by the due date. The recommended procedure is to download and print the homework. Fill in your solutions. Then scan the document and upload to Canvas Assignments. If this is not feasible, you may solve the problems on your paper, scan your solutions, then upload to Canvas. Neatness and presentation are important.
Late homework not accepted. Show all work. Total points: 30
1) Let X1 . . . , Xn be iid N(µ, 16) where σ2= 16 is known. We wish to test the simple hypotheses 美国统计代写
H0 : µ = 2
H1 : µ = 4
Find the sample size n for which the most powerful test will have α = β = 0.01.
Round n to the next largest integer.
Here α is the size of the test which is P(Type I Error) = P(Reject H0|H0 True)and β is P(Type II Error) = P(Fail to reject H0|H0 False).
Hint: What is the distribution of when H0 is true? When H1 is true?
What is β? Drawing a picture may help. (4 points)

2) Consider the simple linear regression model
yi = α + β xi + ∈i , ∈i ∼ N(0, σ2 ) independent
i = 1, . . . , n
Let and
be the sample means of the xi and yi , respectively. In addition, let
and
be the MLEs of α and β, respectively. Let ˆyi =
+
xi be the fifitted values, and let ei= yi − yˆi be the residuals.
a) Find Cov(,
) . (3 points)
b) Show that = 0. (3 points)
c) Show that if = 0, then Cov(
,
) = 0. (2 points)
3) Consider again the simple linear model 美国统计代写
i = 1, . . . , n
a) Using the notation in our lecture notes, the sample correlation coeffiffifficient is defifined as
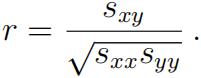
Derive an expression for r in terms of βˆ, sxx, and syy. Do r and βˆ have the same sign?(3 points)
b) In class, we saw that syy = SSR + SSE. That is,
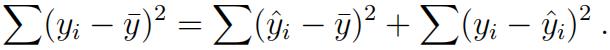
Derive an expression for
in terms of βˆ, sxx, and syy and show that it equals r 2 that you derived in 3a). Hint: Start
with the expression for the fifitted values on page 4 of Lecture 15. (4 points)
c) Write the F-statistic that tests H0 : β = 0 as a function of R2. What happens as R2→ 0?What happens as R2 → 1? (3 points)
4) For a 2 × 2 table with data and cell probabilities 美国统计代写
n11, n12, n21, n22 ∼ Multinomial(n; π11, π12, π21, π22)
we found that the likelihood ratio statistic for testing independence is
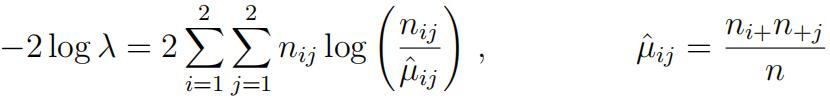
a) Find 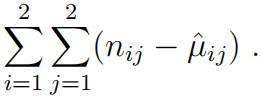
b) Expand
in a second order Taylor series about

Then use the approximation in
to derive the Pearson chi-squared statistic X2 (see Lecture 17). (5 points)Optional problems to try for practice (do not turn in)
Page 363: 12, 13
Page 595: 15
更多代写:加拿大MATH数学代写 雅思保分 计算机code代写 Biology essay代写 Accounting会计论文代写 加拿大统计Final exam代考
合作平台:essay代写 论文代写 写手招聘 英国留学生代写