Stats 426 Spring 2021
Midterm Due 5-28 by 9:25 am EST
统计学代考价格 Solve the problems in the spaces provided and save as a single PDF. Then upload the PDF to Canvas Assignments by the due date.
Instructions: Solve the problems in the spaces provided and save as a single PDF. Then upload the PDF to Canvas Assignments by the due date. The recommended procedure is to download and print the exam. Fill in your solutions. Then scan the document and upload to Canvas Assignments. If this is not feasible, you may solve the problems on your paper, scan your solutions, then upload to Canvas. Neatness and presentation are important. Show all work to receive credit. If supporting work is not shown, the problem will be marked wrong,even if the answer is correct. Use provided tables as needed. Total points: 60
1) Let X ∼ N(µ, σ2 ). Find the probability density function (pdf) of
Y =
Defifine the support of the pdf. (6 points)
2) Let Y1, . . . , Yn be independent and identically distributed random variables each with probability density N(0, θ). The MLE of θ is 统计学代考价格
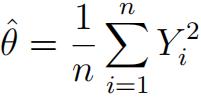
a) Find E[]. Is
unbiased ? (4 points)
b) Find the mean squared error MSEθˆ(θ). Is a consistent estimator ? (5 points)
c) Does achieve the Cramer-Rao Lower Bound (CRLB) ? Give supporting evidence.(7 points)

3) Let Y1, . . . , Yn be independent and identically distributed random variables each with density 统计学代考价格
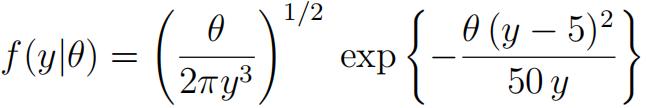
a) Find the MLE of θ. (6 points)
b) State a result about the asymptotic distribution of the MLE as n → ∞ and fifind it.(7 points)
c) Find a suffiffifficient statistic for θ. (6 points) 统计学代考价格
d) Suppose the MLE = 10 and n = 200. Find an approximate 95% confifidence interval for θ. The fifinal answer should be a numeric interval. (4 points)
4) Let Y1, . . . , Y16 be independent and identically distributed random variables each with density N(µ, σ2 ) so that n = 16.
Calculate P(| − µ| < 1.96 σ/4 , 15S2/σ2 < 25). (6 points)5) Let Y be a random variable with probability density function
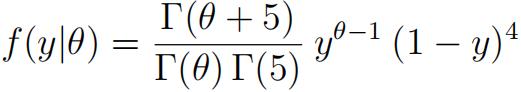
a) Determine if this distribution belongs to the exponential family. If it does, identify c(θ),T(y), d(θ), and S(y). (6 points)
b) Now, suppose Y1, . . . , Yn are independent and identically distributed random variables with pdf f(y|θ). Find a suffiffifficient statistic for θ. (3 points)
更多代写:网课代上北美 gmat代考价格 统计final quiz代考 补充文书Essay代写 北美代写论文 英国统计作业代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写



