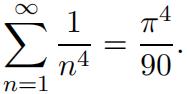Midterm 2
数学原理代考 Throughout this exam, you may use any theorems from class, class assignments, or in the class textbook Chapters 1-9
Throughout this exam, you may use any theorems from class, class assignments, or in the class textbook Chapters 1-9, for which a proof has been provided.
Question 1: Fourier Series
Consider the function, f : [−π, π] → R, given by f(x) = 1 −
1.Show that the Fourier Series of f(x) is given by:
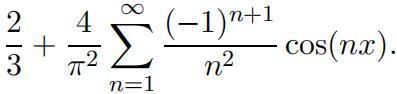
2.From 1., prove:
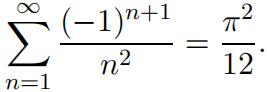
3.From 1., prove:

Question 2: Multivariate Difffferentiation 数学原理代考
Consider the function : R2 → R2:
(x, y) = (x2 − y2, 2xy).
1.Relative to the standard basis on R2, show using only the defifinition of the derivative that:
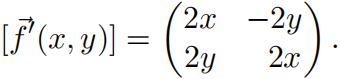
2.Assume a function : U →V,U,V⊂Rn open,admits an inverse
:V→U.
If is difffferentiable at
∈ U, and
is difffferentiable at
(
)∈V,prove that
′ (
) is invertible.
3.Returning to the function (x, y) = (x2 − y2, 2xy), we defifine E ⊂ R2:
E := {(x, y) ∈ R2 ∈ admits alocal C1 inverse in a neighborhood of (x, y)}.
Find the set E ⊂ R2 (Hint: use 2.). Showis not one-to-one on E.
Question 3: Multivariate Difffferentiation (cont.) 数学原理代考
Consider the function f : R3 → R:
f(x, y, z) = x3z + ex − y2.
1.Show that f(0, 1, 2) = 0, (0, 1, 2)≠0,and that there therefore exists a difffferentiable function g in some neighborhood of (1,2) ∈R2, such that g(1, 2)=0, and
f(g(y, z), y, z) = 0.
2.Find that f(1, 2), (0, 1, 2)≠0,and that there therefore exists a difffferentiable function g in some neighborhood of (1,2) ∈R2, such that g(1, 2)=0, and
f(g(y, z), y, z) = 0.
2.Find(1, 2),
(1, 2).
更多代写:历史Online exam代考 duolingo代考 理工作业代写 留学Report代写 留学论文精修机构 英国硕士毕业论文代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写