Final Exam (MTH 252)-Spring 2023
微积分代考 Evaluate ∫∫ xz dS, where S is the boundary of the region enclosed by the cylinder y2 + z2 = 1 and the planes y + x = 5 and x = 0.
Final Exam of MTH 252 will be on May 10, from 10:15 am to 12:15 pm and covers
- Sections 12.4 and 12.5;
- Sections 14.1-14.7;
- Sections 15.1-15.3, 15.5-15.8;
- Sections 16.1-16.9.
I will hold offiffiffice hours on Tuesday (May 09) from 3:00-4:30 pm over zoom. You can reserve a time using the link of offiffiffice hours in the syllabus.
Below are some problems to practice for the fifinal exam. For practice problems for chapter 15 and sections 16.1-16.3, you can use the study guide for Exam 3. Below are some problems to practice for sections 16.4-16.9 and Chapters 12 and 14. The solutions of Questions 10-20 can be found in the study guides for Exams 1-2.
1.Evaluate ∫∫S curl  · dS, where
· dS, where  (x, y, z) = 〈 xz, yz, xy〉 and S is the part of the sphere x2 + y2+ z2= 4 that lies inside the cylinder x2 + y2 = 1 and above the xy-plane.
(x, y, z) = 〈 xz, yz, xy〉 and S is the part of the sphere x2 + y2+ z2= 4 that lies inside the cylinder x2 + y2 = 1 and above the xy-plane.
2.Evaluate C
·
, where
(x, y, z) = 〈 2y, xz, x + y〉 and C is the curve of intersection of the plane z = y + 2 and the cylinder x 2 + y 2 = 1.
3.Evaluate ∫∫ · dS for the vector fifield
(x, y, z) = 〈 z, y, zx〉 and S is the surface of the tetrahedron enclosed by the coordinate planes and the plane x/a + y/b + z/c = 1, where a, b, and c are positive numbers.
4.Evaluate ∫∫ · dS for the vector fifield
· dS for the vector fifield  (x, y, z) = 〈 x4 , −x3 z2 , 4xy2 z〉 and S is the surface of the solid bounded by the cylinder x2 + y2 = 9 and the planes z + x = 2 and z = 0. 微积分代考
(x, y, z) = 〈 x4 , −x3 z2 , 4xy2 z〉 and S is the surface of the solid bounded by the cylinder x2 + y2 = 9 and the planes z + x = 2 and z = 0. 微积分代考
5.Evaluate ∫∫ · dS for the vector fifield
(x, y, z) = 〈 y, z − y, x〉 and the oriented surface S the tetrahedron with vertices (0, 0, 0), (1, 0, 0), (0, 1, 0), and (0, 0, 1) in two ways: 1) using the defifinition of the flflux integral and 2) the divergence theorem.
6.Evaluate ∫∫ xz dS, where S is the boundary of the region enclosed by the cylinder y2 + z2 = 1 and the planes y + x = 5 and x = 0.
7.Evaluate  C
C  · d~r, where
· d~r, where  (x, y) = 〈 e −x + y2 , e−y + x2 〉 and C consists of of the arc of the curve y = cos x from (−π/2, 0) to (π/2, 0) and the line segment from (π/2, 0) to (−π/2, 0).
(x, y) = 〈 e −x + y2 , e−y + x2 〉 and C consists of of the arc of the curve y = cos x from (−π/2, 0) to (π/2, 0) and the line segment from (π/2, 0) to (−π/2, 0).
8.Suppose that C is the oriented curve pictured in the fifigure below.
(a) If (x, y) = (x4 y5 − 2y)~i + (3x + x5 y4 )~ j, evaluate
C
·
(b) If (x, y) = (xy2 − 2y)~i + (3x + y)~ j, evaluate
C
·
ds.
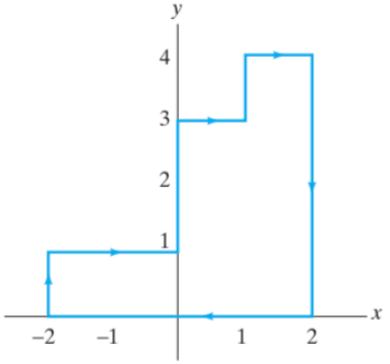
9.Evaluate C
·
, where
(x, y, z) = 〈 xy, yz, zx〉 and C is the boundary of the part of the paraboloidz = 1− x2− y2 in the fifirst ontant.
10.Evaluate ∫∫s curl  ⋅ dS, where F~(x, y, z) = 〈 tan−1 (x2 yz2 ), x2 y, x2 z 2〉 and S is the cone
⋅ dS, where F~(x, y, z) = 〈 tan−1 (x2 yz2 ), x2 y, x2 z 2〉 and S is the cone
x =0 ≤ x ≤ 2, oriented in the the direction of positive x-axis.
11.Find the equation of the plane that contains the line
x = 1 + t, y = 2 − t, z = 4 − 3t
and is parallel to the plane 5x + 2y + z = 1.
12.Find the equation of the plane that contains the line
x = 4 − t, y = 2t − 1, z = −3t
and passes through P(3, 5, −1).

13.Determine whether the lines
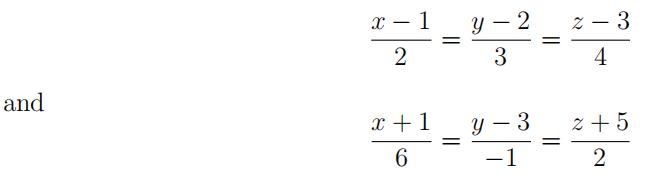
are parallel, skew, or intersecting.
14.Find the limit if it exists or show that it does not exist:
(a) lim(x,y)→(0,0)(x2 + y2 ) ln(x2 + y2 ).
(b) lim(x,y)→(0,0)
15.Find the fifirst partial derivatives of the following functions:
(a) f(x, y) =
(b) p(u, v, w) = u arctan(v )
16.Find the equations of the tangent plane and normal line to the following surfaces at the given point: 微积分代考
(a) xy + yz + zx = 3 at (1, 1, 1).
(b) z = 3x2 − y2 + 2x at (1, −2, 1).
17.Find the points on
x2 + 4y2 − z2 = 4
where the tangent plane is parallel to the plane 2x + 2y + z = 5.
18.Find the maximum and minimum rates of change of f at the given point and the direction in which they occur:
(a) f(x, y) = sin(xy) at P(1, 0).
(b) f(x, y, z) = x ln(yz) at (1, 2, 1).
19.Find critical points of
f(x, y) = (x2 + y2 )e−x.
Then classify them as local maximums, minimums, or saddle points.
20.Suppose f is a difffferentiable function of x and y and
g(u, v) = f(eu + sin v, eu + cos v).
Use the table below to calculate gu(0, 0) and gv(0, 0).
21.(6 points) If z = sin(x + sin t) show that
zxzxt = ztzxx.
更多代写:澳洲网课代上价格 雅思网考 北美online exam代考 英国毕业论文格式 论文数据分析 金融理论与公司政策代考
合作平台:essay代写 论文代写 写手招聘 英国留学生代写




