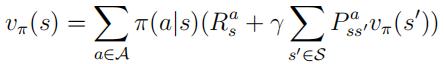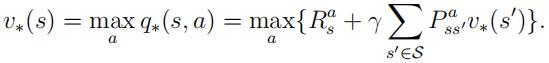Midterm Exam
ELEN E6885: Introduction to Reinforcement Learning
强化学习代考 If the only difference between two MDPs is the value of discount factor γ, then they must have the same optimal policy.
Formula Sheet
1.Bellman expectationequation:
2.Bellman optimalityequation:
3.TD(0)iteration:
v(st) ← v(st) + α(rt+1 + γv(st+1) − v(st)).
Problem 1 (20 Points, 2 Points each)
True or False. No explanation is needed.
- Reinforcementlearning uses the formal framework of Markov decision processes (MDP) to define the interaction between a learning agent and its environment in terms of states, actions and rewards.
- MDP instances with small discount factors tend to emphasize near-term rewards.
- Ifthe only difference between two MDPs is the value of discount factor γ, then they must have the same optimal policy.
- Bothϵ-greedy policy and Softmax policy will balance between exploration and exploitation.
- Everyfinite MDP with bounded rewards and discount factor γ [0, 1) has a unique optimal policy.
- In practice, both policy iteration and value iteration are widely used, and it is not clear which,if either, is better in general. 强化学习代考
- Generalized policy iteration (GPI) is a term used to refer to the general idea of letting policy-evaluationand policy improvement processes interact, independent of the granularity and other details of the two processes.
- Sarsaconverges with probability 1 to an optimal policy and action-value function as long as all state–action pairs are visited an infinite number of times and the policy converges in the limit to the greedy policy.
- Inpartially observable Markov decision process (POMDP), it is likely that an agent cannot identify its current So the best choice is to maintain a probability distribution over the states and actions. and then updates this probability distribution based on its real-time observations.
- Manyoff-policy methods utilize importance sampling, a general technique for estimating expected values under one distribution given samples from another.

Problem 2 (20 Points, 5 Points each) 强化学习代考
Short-answer questions.
- Considera 100×100 grid world domain where the agent starts each episode in the bottom- left corner, and the goal is to reach the top-right corner in the least number of steps. To learn an optimal policy to solve this problem you decide on a reward formulation in which the agent receives a reward of +1 on reaching the goal state and 0 for all other Suppose you try two variants of this reward formulation, (P1), where you use discounted returns with γ (0, 1), and (P2), where no discounting is used. As a consequence, a good policy can be learnt in (P1) but no learning in (P2), why?
- Supposethe reinforcement learning player was Might it always learn to play better, or worse, than a nongreedy player?
- Isthe MDP framework adequate to usefully represent all goal-directed learning tasks? Can you think of any clear exceptions?
- Givena stationary policy, is it possible that if the agent is in the same state at two different time steps, it can choose two different actions? If yes, please provide an example.
Problem 3 (30 Points)
Consider a 2-state MDP. The transition probabilities for the two actions a1 and a2 are summa- rized in the following two tables, where the row and column represents from-state and to-state, respectively. For example, the probability of transition from s1 to s2 by taking action a1 is 0.8.The reward function is Assume the discount factor γ = 0.5.
Table 1: Transition probabilities
- [10Pts] Let v1∗, v2∗ denote the optimal state-value function of state s1, s2, respectively. Write down the Bellman optimality equations with resepect to v1∗ and v2∗.
- [6Pts] Based on your answer to the previous question, prove that v1∗ > v2∗.
- [14Pts] Based on the fact that v1∗ > v2∗, find out the optimal value function v1∗ and v2∗. And write down the optimal policy of this MDP.
Problem 5 (30 Points) 强化学习代考
Consider an undiscounted MDP (γ = 1) with two non-terminal states A, B and a terminal state C. The transition function and reward function of the MDP are unknown. However, we have observed the following two episodes:
A, a1, −1, A, a1, +1, A, a2, +3, C,
A, a2, +1, B, a3, +2, C,
where a1, a2, a3 are actions, and the number after each action is an immediate reward. For example, A, a1, −3, A means that the agent took action a1 from state A, received an immediate
reward −3 and ended up in state A. 强化学习代考
- [9Pts] Using a learning rate of α = 0.1, and assuming initial state values of 0, what updates to V (A) does on-line TD(0) method make after the first episode?
- [10Pts] Draw a diagram of an MDP and policy π that can best fit these two episodes (i.e., the maximum likelihood Markov model). Write down the transition probability P a ′ , the reward function Ra of the MDP you draw, and your estimated policy π(a|s).
- [6Pts] Based on your results in the previous question, solve Bellman equation to find out the state-value function of Vπ(A) and Vπ(B). (Assume Vπ(C) = 0 as state C is the terminal state.)
- [5Pts] What value function would batch TD(0) find, e., if TD(0) was applied repeatedly to these two episodes?
更多代写:Astronomy代考 托福家庭版 Accounting Analysis会计代考 Critical Essay代写 Accounting会计论文代写 paper如何选题
合作平台:essay代写 论文代写 写手招聘 英国留学生代写