MACM 201 – D100 AND D200 ASSIGNMENT #7
加拿大数学代写 Answer all questions on paper or a tablet using your own handwriting. Put your name, student ID number and page number at the top of each page.
Instructions
Answer all questions on paper or a tablet using your own handwriting. Put your name, student ID number and page number at the top of each page. If you use paper make a photo of each page and upload your solutions to crowdmark. If you use a tablet, export your assignment to .pdf and upload the .pdf to crowdmark.
Textbook Reading
- Sections: 11.4, 11.5, 12.1
Exercises
A.Textbook Questions
11.4 Exercises 2, 14ad, 26abc.
11.5 Exercises 1, 6.
12.1 Exercises 4, 6, 10
B.Instructor Questions 加拿大数学代写
Questions on 11.4
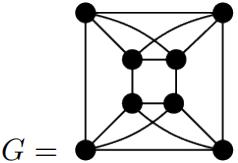
1.Find a subgraph of the graph G below that is subdivision of K3,3. Conclude that G is not planar.
2.Let G = (V, E) be a connected simple graph with |V | ≥ 11.
Show that G or its complementis not planar.
3.Draw a planar embedding of the tetrahedron T. Draw T∗ the dual of T.

Questions on 11.5
4.Recall that Km,n denotes the complete bipartite graph with m + n vertices.
(a) Does K2,3 have a Hamiltonian cycle? If yes draw one. If not explain.
(b) Does K2,3 have a Hamiltonian path? If yes draw one. If not explain.
(c) Find the Km,n with the fewest vertexes which has a Hamiltonian cycle.
(d) Find the Km,n with the fewest vertexes which has a Hamiltonian path.
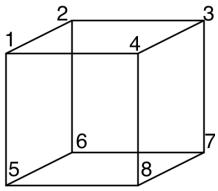
5.Below is a non-planar drawing of the cube graph. 加拿大数学代写
Draw a planar embedding of the cube graph.
Draw all Hamiltonian cycles that include the edge {1, 2}. I found four.
6.What is the converse of Theorem 11.8?
Give a counter example to the converse of Theorem 11.8.
Questions on 12.1 加拿大数学代写
7.If a tree has four vertices of degree 2, four of degree 4, and two of degree 5, how many pendant vertices does it have?
8.In class we proved the following theorem:
If T = (V, E) is a tree and u, v ∈ V are distinct, there is a unique path in T from u to v.
Prove that the converse of the theorem is also true, namely
Let G = (V, E) be a simple graph. If for every pair of vertices u, v ∈ V there is a unique path in G from u to v then G is a tree.
更多代写:北美代考多少钱 gmat保分 澳大利亚Econ网课代考 Scientific Essay代写 澳洲实验报告代写 美国数学作业代做
合作平台:essay代写 论文代写 写手招聘 英国留学生代写