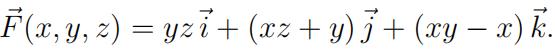Exam 3 (MTH 252)-Spring 2023
加拿大微积分Final exam代考 Determine whether or not the following vector fifield is conservative. Explain your rea-soning well to support your claims.
Exam 3 will be on April 19 and covers Sections 15.3-15.9 (except 15.4) and 16.1-16.3.You should review your class notes and examples discussed during our meetings. I will hold a review session for the exam on Tuesday from 4:00-5:30 pm in BAC 245. Below are some problems to practice for the exam. We will discuss some of these problems during the review session.
1.Evaluate each integral:
(a) A with R = {(x, y)| x2 + y2 ≤ 4, x ≥ 0, y ≥ 0}.
(b)
2.Find the volume of the following solids.
(a) The solid bounded by the paraboloids z = x2 + y2 and z = 2 − x2 − y2 .
(b) The solid bounded by the cylinder x2 + y2 = 4 and z = 3 − x and z = x − 3.
3.Find the area of the part of the sphere x2 + y2 + z2 = 4 that lies above the plane z = 1.
4.Rewrite the integral 加拿大微积分Final exam代考
as an iterated integral in the order dydzdx.
5.Rewrite the integral
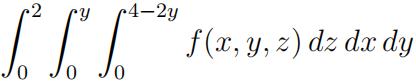
as an iterated integral in the order dy dz dx and dx dy dz.
6.Evaluate each integral:
(a) where E is bounded by the paraboloid x = 4y2 + 4z2 and the plane x = 4.
(b) where E is enclosed by the surfaces z = x2 − 1 and z = 1 − x2 ,y = 0,y = 2.

7.Find the volume of the solid that is enclosed by the cone z = p x2 + y2 and the sphere 加拿大微积分Final exam代考
x2 + y2 + z2 = 2.
8.Evaluate where E is the solid that lies within both the cylinder x2+y2 = 1 and x2 +y2 = 16 above the
xy-plane and below the plane z = y + 4.
9.Evaluate 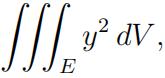
10.Evaluate the integral  where R is the region with vertices (1, 0), (2, 0),(0, 2), and (0, 1).
where R is the region with vertices (1, 0), (2, 0),(0, 2), and (0, 1).
11.Evaluate the integral 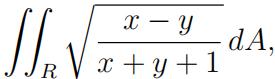
12.Evaluate the integral 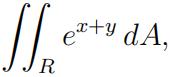
13.Find the volume of the solid outside the cone φ = π/4 and inside the sphere ρ = 4 cos φ. 加拿大微积分Final exam代考
14.Find the volume of the part of ρ ≤ 2 that lies between the cones φ = π/3 and φ = 2π/3.
15.Show that the line integral where
and C is any path from (1, 0) to (2, 1), is independent of path and then evaluate the integral.
16.Determine whether or not the following vector fifield is conservative. Explain your rea-soning well to support your claims.
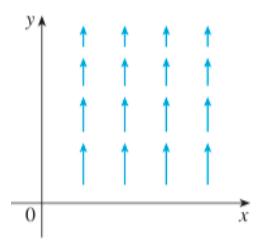
17.Determine wether or not the vector fifield is conservative. If it is conservative, fifind a function f such that = ∇f.
18.Assume (x, y) = 〈 3x2 + y2 , 2xy〉 and C is the curve shown below: 加拿大微积分Final exam代考
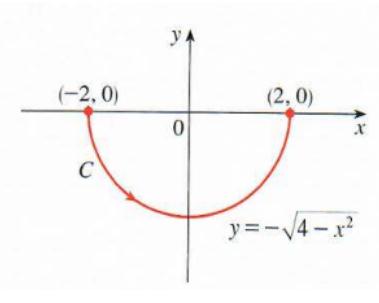
(a) Evaluate∫C⋅dr.
(b) Show that is conservative and fifind a function such that
= ∇f.
(c) Evaluate ∫C · dr using the Fundamental Theorem of Calculus for line integrals.
(d) Evaluate ∫C · dr by fifirst replacing C by a simpler curve that has the same initial and terminal points.
19.Evaluate R C (x 2+y 2 +z 2 )ds, where
C is the curve with parametric representation (t) =〈 t, cos 2t,sin 2t〉and 0≤ t ≤ 2π.
20.The fifigure shows a vector fifield F~ and two curves C1 and C2. Are the line integrals of over C1 and C2 positive, negative, or zero? Explain.
更多代写:加拿大Finance代写 gmat线上代考 计量经济学网课代刷 会计Essay代写论文 记叙文essay代写 微积分代考
合作平台:essay代写 论文代写 写手招聘 英国留学生代写
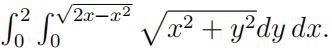

 where R is the region with vertices (1, 0), (2, 0),(0, 2), and (0, 1).
where R is the region with vertices (1, 0), (2, 0),(0, 2), and (0, 1).