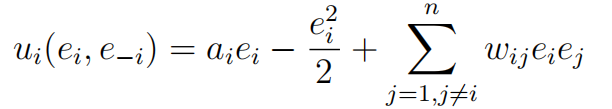SUMMER TERM 2017
ECON3014: GAME THEORY
TIME ALLOWANCE: 2 hours
代考GAME THEORY Two fifirms are competing with each other by setting prices for their product (they produce identical homogeneous product).
Answer any THREE questions. All questions carry equal weight.
In cases where a student answers more questions than requested by the examination rubric, the policy of the Economics Department is that the student’s fifirst set of answers up to the required number will be the ones that count (not the best answers). All remaining answers will be ignored.
1.Consider a game of n players in which each player chooses an effffort level ei ≥ 0, i = 1, .., n.The marginal benefifit of effffort for player i depends on the effffort exerted by the other players. In particular, the payoffff of player i is 代考GAME THEORY
where parameters ai > 0, wij ≥ 0 are commonly known for all i and j. The players choose their effffort levels simultaneously and independently.
(a) Solve for a best reply of player i.
(b)Assume that ai = a > 0 and wij = w for all i, j. Provide the conditions under which symmetric NE in pure strategies exists. Provide intuition for your result. 代考GAME THEORY
(c) Assume that n = 3, ai = a > 0. Consider two situations: fifirst w12 = w23 = w13 = w,and second w12 = w23 = w, w13 = 0. Assuming that 0 < w < 1/2, compare the equilibrium effffort level of player 2 in these two situations (you may impose reasonable symmetry assumptions on equilibrium). Provide intuition for your result.

2.Two players are playing a game “21”. At the beginning of the game player 1 starts by saying number “1”. Then players take turns and increase the number by either 1, 2 or 3.A player that is forced to say a number that is larger or equal to 21 loses and his opponent wins. 代考GAME THEORY
(a) Formalize this game. Defifine the most appropriate solution concept for it.
(b) Solve for all equilibria of this game.
(c) Consider a modifification of this game in which a player that is forced to say a number that is larger or equal to 2001 loses. Which player wins the game in equilibrium?Explain your answer.
3.Two fifirms are competing with each other by setting prices for their product (they produce identical homogeneous product). 代考GAME THEORY
Firm i can produce the good at marginal cost ci , i = 1, 2(these costs are commonly known). There are two periods. Firm 1 sets its price in period1 and once the price is announced it cannot be changed until the end of time. Firm 2 does not participate in the market in period 1; it enters the market at period 2 by setting its own price. Consumers always choose to buy from the fifirm whose price is the lowest. If the prices offffered by two fifirms are equal, all the consumers buy from fifirm 2. The demand for a product in each period is
Q = A − P.
Both fifirms maximize the sum of their own profifits across periods.
(a) Assume that 0 < c2 < c1 < A. Find an equilibrium. 代考GAME THEORY
(b) Assume that 0 < c1 < c2 < A. Find an equilibrium.
(c) Assume that marginal cost of fifirm 2 is drawn randomly from a uniform distribution with the support on [0, A]. Find an equilibrium.
4.Consider a game between a policymaker and an advisor. A nature chooses a state of the world x ∈ [0, 1] according to a uniform distribution and informs the advisor of this state.
The advisor sends a message m ∈ [0, 1] to the policymaker and the policymaker sets a policy y ∈ [0, 1] after receiving the message. The policymaker and the advisor maximize the following utility functions respectively:
u(x, y) = −(x − y)2
u(x, y) = −(αx − y)2
where α ∈ (0, 1) is a known parameter that is close to 1.
(a) Find the ideal policies for the policymaker and the advisor conditional on some information I that they have about the state of the world. 代考GAME THEORY
(b) Show that there exists no separating equilibrium in this game.
(c) Find a partially separating equilibrium in which the advisor uses only two messages.Provide conditions that guarantee the existence of this equilibrium.
更多代写:Coursework课程作业代写 思培代考 cs代写机构 留学个人陈述 曼切斯特论文辅导 duolingo考试作弊
合作平台:essay代写 论文代写 写手招聘 英国留学生代写