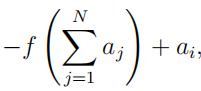SUMMER TERM 2020
24-HOUR ONLINE EXAMINATION
ECON0027: GAME THEORY
代考博弈论 Your answer should not exceed this page limit. This page limit is generous to ac-commodate students with large handwriting.
All work must be submitted anonymously.
Please ensure that you add your candidate number and the module code to the template answer sheet provided. Note that the candidate number is a combination of four letters plus a number, e.g. ABCD9. You can fifind your candidate number in your PORTICO account, under My Studies then the Examinations container. Please, note that the candidate number is NOT the same as your student number (8 digits), which is printed on your UCL ID card. Submitting with your student number will delay marking and when your results might be available.
Page limit: 12 pages
Your answer should not exceed this page limit. This page limit is generous to ac-commodate students with large handwriting. We expect most of the submissions to be signifificantly shorter than the set page limit. If you exceed the maximum number of pages, the mark will be reduced by 10 percentage points, but the penalised mark will not be reduced below the pass mark: marks already at or below the pass mark will not be reduced.
Answer ALL questions. All questions carry equal weight. 代考博弈论
Allow enough time to submit your work. Waiting until the deadline for submission risks facing technical problems when submitting your work, due to limited network or systems capacity.
By submitting this assessment, you pledge your honour that you have not violated UCL’s Assessment Regulations which are detailed in https://www.ucl.ac.uk/academic- manual/chapters/chapter-6-student-casework-framework/section-9-student-academic-misconduct-procedure
which include (but are not limited to) plagiarism, self-plagiarism, unauthorised collab-oration between students, sharing my assessment with another student or third party,access another student’s assessment, falsifification, contract cheating, and falsifification of extenuating circumstances.
1.Sonic the hedgehog wants to purchase running shoes from Dr Robotnik. It is commonly known that Sonic values the shoes at v and Dr Robotnik’s cost of procuring the shoes is zero. 代考博弈论
Dr Robotnik chooses a price and makes an offffer to Sonic. Sonic can either accept the offffer or decline it. If Sonic accepts, he pays Dr. Robotnik’s price and gets his shoes. If he declines the offffer, the trade does not occur and the game ends.
(a) Formulate this situation as a game, defifine the appropriate equilibrium notion and solve for all the equilibria of this game.
(b) Suppose that in order for Dr. Robotnik to make his offffer, Sonic has to travel to his laboratory and meet him there. The cost of travel for Sonic is c > 0 (also commonly known). Find all equilibria of this game when c < v. Explain what would change in your analysis if c ≥ v.
(c) Suppose there are a hundred clones of Dr. Robotnik, each with his own laboratory, indexed by i ∈ {1, 2, …100}. Each clone can sell shoes to Sonic(Sonic only needs one pair). Each Robotnik i secretly chooses a price in the beginning of the game. After the prices are chosen, Sonic is randomly placed in one of the hundred laboratories. At a laboratory, the price chosen by its owner is revealed to Sonic. Sonic can either accept it, decline it and travel to another (randomly chosen) laboratory, or decline the offffer, give up the search and end the game. If the offffer is accepted, Sonic pays the price and gets the shoes. If Sonic declines the offffer and travels to another laboratory, he faces a travel cost c. Solve for all pure strategy equilibria of this game. Explain how competition between Robotniks affffects Sonic’s equilibrium payoffff.

2.Two chefs are competing for a position at a restaurant called “Food for Thought”.
The value of the position to each chef is equal to v. The competition takes a form of a contest in which one of the two chefs who bakes a bigger cake wins. In order to bake a cake of size x > 0, chef i has to procure x kilograms of flflour from the restaurant at a price pi . The restaurant will charge a chef for the flflour only if he wins the contest. The price of flflour pi for each chef i is drawn randomly from a uniform distribution on [1, 2]. The prices for the two chefs are independent.The chefs choose the sizes of their cakes simultaneously to maximize the expected value of the position net of the expenses for the flflour. 代考博弈论
(a) Suppose the realized prices for the flflour are publicly observed before the chefs make their choices. Let p1 < p2 and suppose that in the event the chefs bake the cakes of equal size, the chef who can source cheaper flflour—i.e., chef 1—wins. Find a Nash equilibrium of this game.
(b) Suppose the chefs privately observe the realization of their prices: chef observes only p1 and chef 2—only p2. Solve for a Bayes-Nash equilibrium of the game.
(c) Continue assuming that the chefs privately observe the realization of their prices. In addition, suppose that the restaurant charges chefs for the flflour independently of the contest outcome. Solve for a Bayes-Nash equilibrium of the game.
3.Consider the following modifified beer-and-quiche game
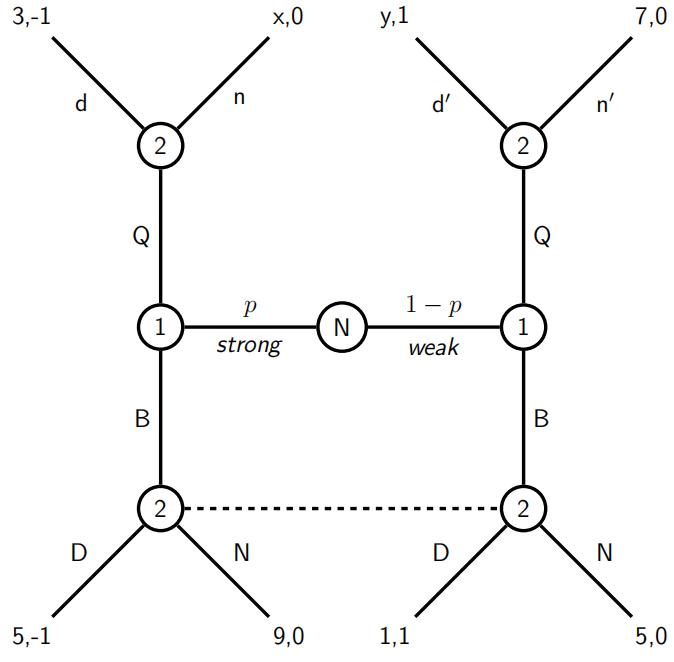
(a) Suppose y = 3 and x = 7. Find all weak sequential equilibria of this game.
(b) Suppose y = 3. Find all values of x such that there is an equilibrium in which both types of player 1 play B.
(c) Suppose x = 7. Find all values of y such that there is an equilibrium in which difffferent types of player 1 play difffferent pure actions.
4.Consider an outbreak of an infectious disease that is transmitted in a human-to-human interaction. 代考博弈论
There is a society of N individuals. Each individual i independently chooses a level of an economic activity ai ≥ 0. The economic activity is valuable for the individual, but it facilitates the spread of the infection.
The payoffff of an individual i is
where the fifirst part is the expected cost of being infected which is increasing in the total economic activity in the society, and the second part is the individual benefifit of the economic activity. Assume that f is twice continuously difffferentiable, f ‘ (x) > 0 and f ” (x) > 0 for all x. Also, assume that f ‘ (0) = 0 and
(a) Formulate this situation as a game. Defifine the equilibrium notion that is the most appropriate. Find all symmetric equilibria in this game.
(b) Find the symmetric Pareto-effiffifficient outcome in this game. In order to do that, solve the social planner’s problem in which the social planner treats the population symmetrically. Compare your answer to your fifindings in question 4a. Explain the economic intuition behind this comparison.
更多代写:代写作业Assignment代做 pte代考靠谱吗 北美英文作业代写 北美文献综述代写 伯明翰大学论文代写 文书essay代写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写