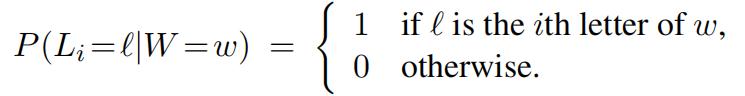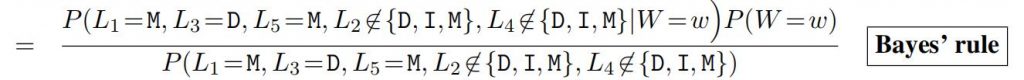Intro to AI. Assignment 2
人工智能代写 A patient is known to have contracted a rare disease which comes in two forms, represented by the values of a binary random variable D ∈ {0, 1}.
2.1 Probabilistic reasoning 人工智能代写
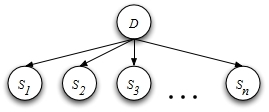
A patient is known to have contracted a rare disease which comes in two forms, represented by the values of a binary random variable D ∈ {0, 1}. Symptoms of the disease are represented by the binary random variables Sk ∈ {0, 1}, and knowledge of the disease is summarized by the belief network:
The conditional probability tables (CPTs) for this belief network are as follows. In the absence of evidence, both forms of the disease are equally likely, with prior probabilities: P (D = 0) = P (D = 1) = 1 . In one form of the disease (D = 0), all the symptoms are uniformly likely to be observed, with P (Sk = 0 D = 0) = 1 for all k. By contrast, in the other form of the disease (D = 1), the first symptom occurs with probability one,
P (S1 = 1|D = 1) = 1,
while the kth symptom (with k ≥ 2) occurs with probability
where the function f (k) is defined by
f (k) = 2k + (−1)k.
Suppose that on the kth day of the month, a test is done to determine whether the patient is exhibiting the kth symptom, and that each such test returns a positive result. Thus, on the kth day, the doctor observes the patient with symptoms S1 = 1, S2 = 1, . . . , Sk = 1 . Based on the cumulative evidence, the doctor makes a new diagnosis each day by computing the ratio:
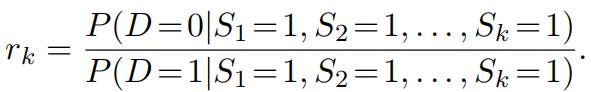
If this ratio is greater than 1, the doctor diagnoses the patient with the D = 0 form of the disease; otherwise, with the D = 1 form.
(a)Compute the ratio rkas a function of k. How does the doctor’s diagnosis depend on the day of the month? Show your work.
(b)Does the diagnosis become more or less certain as more symptoms are observed?
2.2 Noisy-OR 人工智能代写
(a) Conditional probability table
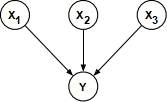
Complete the noisy-OR conditional probability table for the belief network shown above. (The miss- ing values in the table are determined by the ones shown.)
| X1 | X2 | X3 | P (Y = 1|X1, X2, X3) |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | |
| 0 | 1 | 0 | 1
3 |
| 0 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 0 | 1 | |
| 0 | 1 | 1 | 4
5 |
| 1 | 1 | 1 | 5
6 |
(b) Qualitative reasoning
Suppose that each node Xi in this model has some finite, non-zero prior probability to be either zero or one; namely 0 < P (Xi = 1) < 1. Sort the following probabilities from smallest to largest:
P (X2 = 1) P (X2 = 1|Y = 0)
P (X2 = 1|Y = 1)
P (X2 = 1|Y = 1, X1 = 0, X3 = 0)
P (X2 = 1|Y = 1, X1 = 1, X3 = 1)
For this part, you are not required to compute numerical values for these probabilities, only to sort them in ascending order. In fact, this part can be completed independently of the values in part (a).
(c) Quantitative reasoning
Suppose that P (Xi = 1) = 1 for i 1, 2, 3 . Compute numerical values for the probabilities in part (b) from these priors and your answers in part (a). Do these values match your previous ordering?

2.3 Hangman 人工智能代写
Consider the belief network shown below, where the random variable W stores a five-letter word and the random variable Li A, B, . . . , Z reveals only the word’s ith letter. Also, suppose that these five-letter words are chosen at random from a large corpus of text according to their frequency:
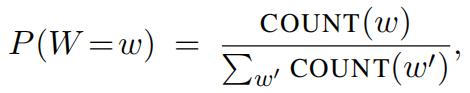
where COUNT(w) denotes the number of times that w appears in the corpus and where the denominator is a sum over all five-letter words. Note that in this model the conditional probability tables for the random variables Li are particularly simple:
Now imagine a game in which you are asked to guess the word w one letter at a time. The rules of this game are as follows: after each letter (A through Z) that you guess, you’ll be told whether the letter appears in the word and also where it appears. Given the evidence that you have at any stage in this game, the critical question is what letter to guess next.

Let’s work an example. Suppose that after three guesses—the letters D, I, M—you’ve learned that the let- ter I does not appear, and that the letters D and M appear as follows:
M D M
Now consider your next guess: call it A. In this game the best guess is the letter A that maximizes
P L2 = or L4 =
L1 = M, L3 = D, L5 = M, L2 ƒ∉ {D, I, M}, L4 ƒ∉ {D, I, M} .
In other words, pick the letter A that is most likely to appear in the blank (unguessed) spaces of the word. For any letter we can compute this probability as follows:
P .L2 = or L4 =
L1 = M, L3 = D, L5 = M, L2 ƒ∈ {D, I, M}, L4 ƒ∈ {D, I, M}Σ
= Σ P .W = w, L2 = or L4 =
L1 = M, L3 = D, L5 = M, L2 ƒ∈ {D, I, M}, L4 ƒ∈ {D, I, M}Σ, marginalization
= Σ P (W = w|L1 = M, L3 = D, L5 = M, L2 ƒ∈ {D, I, M}, L4 ƒ∈ {D, I, M}Σ P (L2 = or L4 = A|W = w) product rule & CI
where in the third line we have exploited the conditional independence (CI) of the letters Li given the word W . Inside this sum there are two terms, and they are both easy to compute. In particular, the second term is more or less trivial:
P (L2 = A or L4 = |W = w) = . 1 if A is the second or fourth letter of w
And the first term we obtain from Bayes’ rule:
P (W = w|L1 = M, L3 = D, L5 = M, L2 ƒ∉ {D, I, M}, L4 ƒ∉ {D, I, M}
In the numerator of Bayes’ rule are two terms; the left term is equal to zero or one (depending on whether the evidence is compatible with the word w), and the right term is the prior probability P (W = w), as determined by the empirical word frequencies. The denominator of Bayes’ rule is given by:
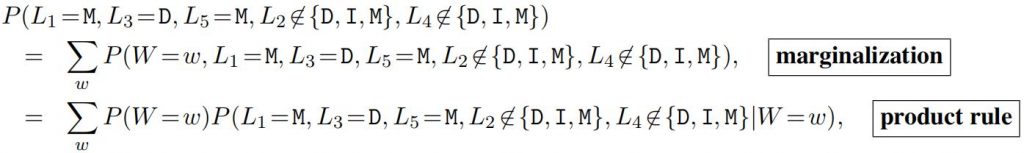
where again all the right terms inside the sum are equal to zero or one. Note that the denominator merely sums the empirical frequencies of words that are compatible with the observed evidence.
Now let’s consider the general problem.
Let E denote the evidence at some intermediate round of the game: in general, some letters will have been guessed correctly and their places revealed in the word, while other letters will have been guessed incorrectly and thus revealed to be absent. There are two essential computations. The first is the posterior probability, obtained from Bayes’ rule:
The second key computation is the predictive probability, based on the evidence, that the letter A appears somewhere in the word:

Note in particular how the first computation feeds into the second. Your assignment in this problem is to implement both of these calculations. You may program in the language of your choice.
(a)Download the file hw2 word counts 05.txt that appears with the homework assignment. The file contains a list of 5-letter words (including names and proper nouns) and their counts from a large corpus of Wall Street Journal articles (roughly three million sentences). From the counts in this file compute the prior probability P (w) = COUNT(w)/COUNTtotal. As a sanity check, print out the tenmost and least frequent 5-letter words. Do your results make sense?
(b)Consider the following stages of the game.
For each of the following, indicate the best next guess— namely, the letter that is most likely (probable) to be among the missing letters. Also report the probability P (Li=
for some i 1, 2, 3, 4, 5 E) for your guess
. Your answers should fill in the last two columns of this table. (Some answers are shown so that you can check your work.)
| correctly guessed | incorrectly guessed | best next guess |
P (Li = |
| – – – – – | {} | ||
| – – – – – | {E, O} | ||
| Q – – – – | {} | ||
| Q – – – – | {U} | ||
| – – Z E – | {A, D, I, R} | ||
| – – – – – | {E, O} | I | 0.6366 |
| D – – I – | {} | A | 0.8207 |
| D – – I – | { |
E | 0.7521 |
| – U – – – | {A, E, I, O, S} | Y | 0.6270 |
(c)Include your source code when you submit to elearning website. Do not forget the source code: it is worth many points on this assignment.
2.4 Conditional independence
For the belief network shown below, indicate whether the following statements of marginal or conditional independence are true (T) or false (F).
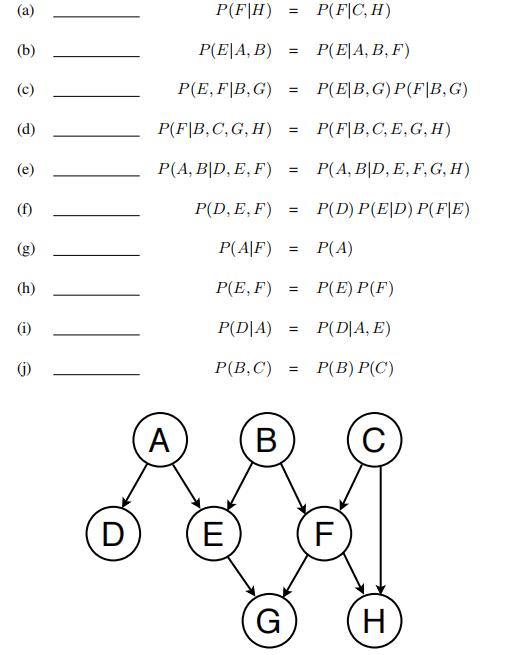
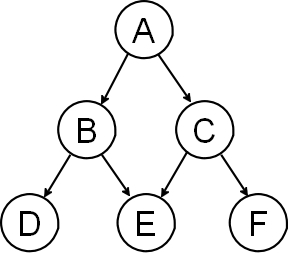
2.5 Subsets
For the DAG shown below, consider the following statements of marginal or conditional independence. Indicate the largest subset of nodes S ⊆ {A, B, C, D, E, F } for which each statement is true. Note that one
possible answer is the empty set S = ∅ or S = {} (whichever notation you prefer).
(a)P(A) = P (A|S)
(b)P(A|C) = P (A|S)
(c)P(A|B, C) = P (A|S)
(d)P(B) = P (B|S)
(e)P(B|A, E) = P (B|S)
(f)P (B|A,C, E) = P (B|S)
(g)P(D) = P (D|S)
(h)P(D|A) = P (D|S)
(i)P(D|C, E) = P (D|S)
(j)P(D|F ) = P (D|S)
更多代写:多线程代写 雅思代考 代做功课推荐 book review怎么写 apa论文格式 essay代写靠谱吗
合作平台:essay代写 论文代写 写手招聘 英国留学生代写