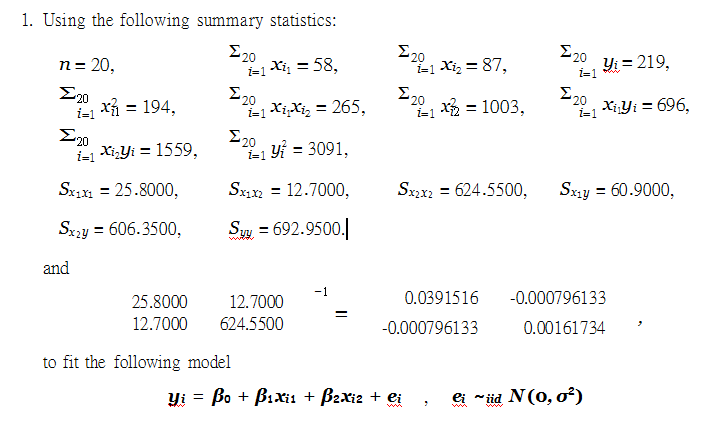博客

MATH3424 Regression Analysis

 Assignment 3

regression-analysis代写 Assume that β0 β1 and β2 is unknown.Re-writethe model to a centered  Find the least squares estimates of the unknown parameters ···

1.Usingthe following summary statistics: regression-analysis代写

Assume that β₀ β₁ and β₂ is unknown.

• Re-writethe model to a centered  Find the least squares estimates of the unknown parameters β₀, β₁ and β₂. Then, write down the fitted line.

• Find the unbiasedestimate of the unknown parameter σ². No need to show that it is

• Constructan ANOVA table and then test H₀: β₁ = β₂ = 0 at significance level of

α = 0.05. Write down your conclusion clearly.

• Testthe null hypothesis that H₀ : β₁ −β₂ = 0 against the alternative hypothesis that

H₁ : β₁ −β₂ ̸= 0 at the significant level of α = 0.05. Construct the test statistic using

1. t-test. Writedown the test statistic, the critical value and your conclusion  regression-analysis代写

1. Ftest in terms of “Increase in Regression Sum of Squares”. Write down the test statistic, the critical value and your conclusion

• Ftest for testing H₀ : C β = d. Write down the test statistic, the critical value and your conclusion

2.Usingthe following data set

to fit a model of y on x₁ and x₂, i.e., do the following regression model,

y_i = β₀ + β₁x_i1 + β₂x_i2 + e_i, e_i ∼ N (0, σ²). regression-analysis代写

From the previous calculation, it is known that βˆ0  = 1.774373, βˆ1  = 1.636212 and βˆ2  = 1.401114.

• Re-writethe model to a centered model in matrix  Define Y and X in terms of data. Write down X^T X, (X^T X)⁻¹ and X^T Y in terms of values of summary statistics.

• FindResidual Sum of Squares and Pure Error Sum of

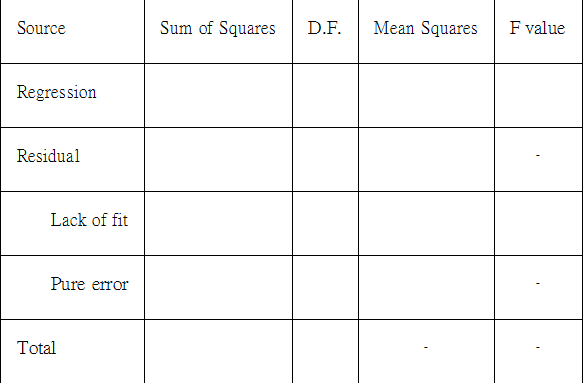
• Fillthe following

1. Conducta lack of fit test at α = 0. Write down your test statistic, critical value and your conclusions clearly.

1. Findthe unbiased estimate of σ² based on the conclusion from the lack of fit test  regression-analysis代写

• TestH₀: β₁ = β₂ = 0 at significance level of α = 0. Write down your test statistic, critical value and your conclusions clearly.

1. Calculatethe coefficient of

• Constructthe 95% predication interval for individual value of y at x₁ = 5 and x₂ =
• Testthe null hypothesis that H₀ : β₁ = β₂ against the alternative hypothesis that

H₁ : β₁ ̸= β₂ by F test at the significance level of α = 0.05.

1. Findthe Residual Sum of Squares of the model under the null
2. Constructthe test statistic in terms of “Increase in Regression Sum of Squares”. Write down the test statistic, the critical value and your conclusion

• Test H₀: β₀ = 1 against the alternative hypothesis H₁ : β₀ = 1 by t-test at the significance level of α = 0. Write down the test statistic, the critical value and your conclusion clearly.
• TestH₀ : β₁ + β₂ = 2 against the alternative hypothesis that H₁ : β₁ + β₂ = 2 by F test for the General Linear Hypothesis at the significance level of α = 0. Write down the test statistic, the critical value and your conclusion clearly.

Hint:  Write down the null hypothesis as H₀ :∼C∼β  = ∼d . regression-analysis代写

• Assumethat β₀ = 1.  Estimate the unbiased estimate of the unknown parameter

σ². No need to show that it is unbiased.

• Assumethat β₀ = 1 and β₁ = β₂. Find the least squares estimate of the unknown parameter in the model. Then, write down the fitted line. Estimate the unbiased estimate of the unknown parameter σ². No need to show that it is

1. Tenmen were studied during a maximal exercise treadmill test. The dependent and independent variables are: y = VO_2max, x₁ = weight, x₂ = HR_max, x₃ = SV_max. The table of parameter estimates, standard error and covariance matrix is given below:

• Find the t-value for testing the statistical significance of β₃= 0. Do we reject β₃ = 0 at the 5% significance level?

• Constructa 95% confidence interval for β₁. regression-analysis代写

• Testwhether the ratio of the regression coefficient of x₂ to that of x₃ is equal to 5 at the 5% significance level. Write down your test statistic, critical value and your conclusions clearly.
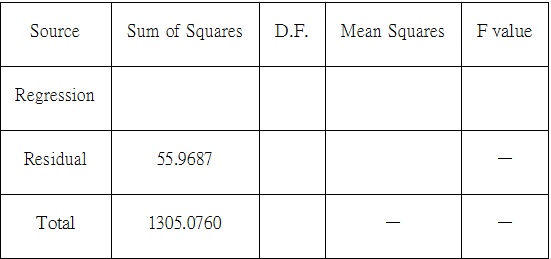
• Fill in the missing values in the analysis of variance table below.Is the regression significant at the 5% significance level?

更多其他：代写作业 数学代写 物理代写 生物学代写 程序编程代写 Visualising Data代写

合作平台：天才代写 幽灵代写  写手招聘  paper代写