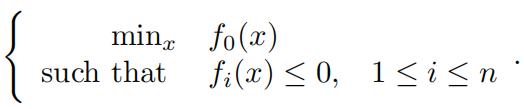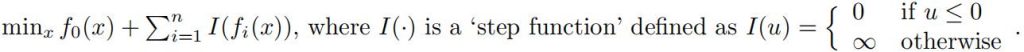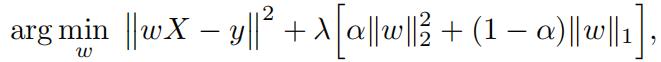COMS 4771002 (Fall 2017) Exam 1 October 19, 2017
Machine Learning代考 Please show all your work! Answers without supporting work will not be given credit. Write your answers in spaces provided.
Please show all your work! Answers without supporting work will not be given credit. Write your answers in spaces provided.
There are total thirteen pages including two blank pages at the end for scratch work. You have 1 hour and 15 minutes to complete this exam.
You may use any result from the lectures or the homeworks without proof.
Name & UNI:
1.(16 points) For each statement below state either True or Justify your answer by providing a short explanation/proof sketch (for true statements) or a counter example (for falsestatements). Machine Learning代考
(a) Bayes classifier (i.e. the optimal classifier) always yields zero classification error.
(b) Kernel regression with a box kernel typically yields a discontinuous predictor.
(c) If we train a Na¨ıve Bayes classifier using infinite training data that satisfies all of its modeling assumptions (e.g., features in the training data are independent given the class labels), then it will achieve zero training error over these training examples. Machine Learning代考
(d) Suppose you are given a dataset of cellular images from patients with and without cancer. If you are required to train a classifier that predicts the probability that the patient has cancer, you would prefer to use Decision trees over Logistic regression.
(e) Given a d × d symmetric positive semidefinite matrix A. The transformation ø : x ›→ xTAx is a linear transformation.
(f) Ordinary Least Squares (OLS) regression is consistent. That is, as the number of samples approaches infinity, OLS error approaches the error of the optimal regressor.
(g) Consider the constraint optimization problem:
This optimization problem is equivalent to the following unconstraint optimization problem:
That is, the optimal solution to the given constraint optimization problem is equal to the optimal solution for the given unconstraint optimization problem.
(h) For any d ≥ 1, the unit L0-ball in Rd, that is, the set {x ∈ Rd : ||x||0 ≤ 1}, is not a convex set.
2.[Maximum Likelihood Estimation and beyond (13 points)]
Your friend gives you a coin with bias b (that is, tossing the coin turns ‘1’ with probability b, and turns ‘0’ with probability 1 − b). You make n independent tosses and get the observation sequence x1, . . . , xn ∈ {0, 1}.
(a)Youwant to estimate the coin’s What is the Maximum Likelihood Estimate (MLE) ˆb given the observations x1, . . . , xn?
(b)Isyour estimate from part (a) an unbiased estimator of b? Justify your answer. Machine Learning代考
(c)Derivea simple expression for the variance of this coin?
(d)Whatis the MLE for the coin’s variance?
(e)Your friend reveals to you that the coin was minted from a faulty press that biased it towards 1. Supposethe model for the faulty bias is given by the following distribution:
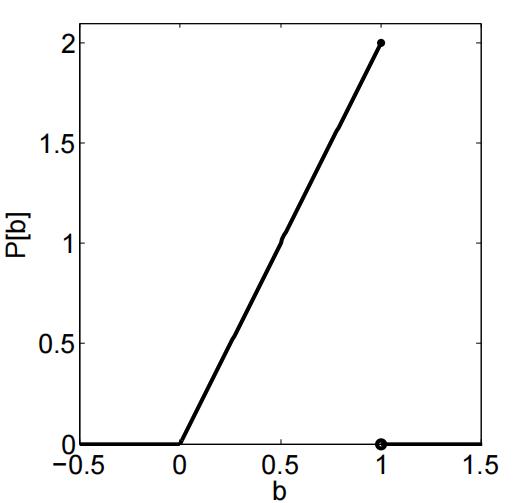
Having this extra knowledge, what is the best estimate for the coin’s bias b given the observation sequence? That is, compute: arg maxb P [b | x1, . . . , xn].
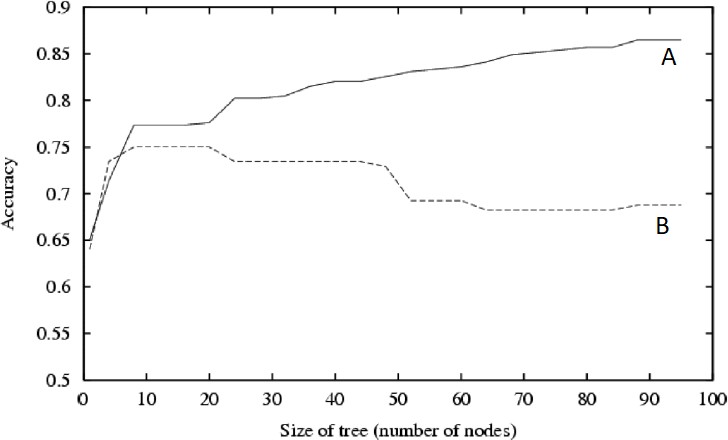
3.[AnalyzingClassifter Performance (6 points)] Consider the plot below showing training and test set accuracy curves for decision trees of different sizes, using the same set of training data to train each tree.
(a)What is the most likely correspondence between the training and test curves, and the curves marked‘A’ and ‘B’ in the figure? Machine Learning代考
(b)Describein one sentence how the training data curve will change if the number of training examples approaches infifinity.
(c)How will the test data curve change under the same condition as in part ii (ie, for the case when number of training examples approachesinfinity)?

4. [Linear Classiftcation]
(a)(3 points) The figure below depicts the decision boundaries of three linear classifiers (labeled A, B, and C) and the locations of labeled training data of n points (positive points are circles, negative points aretriangles).
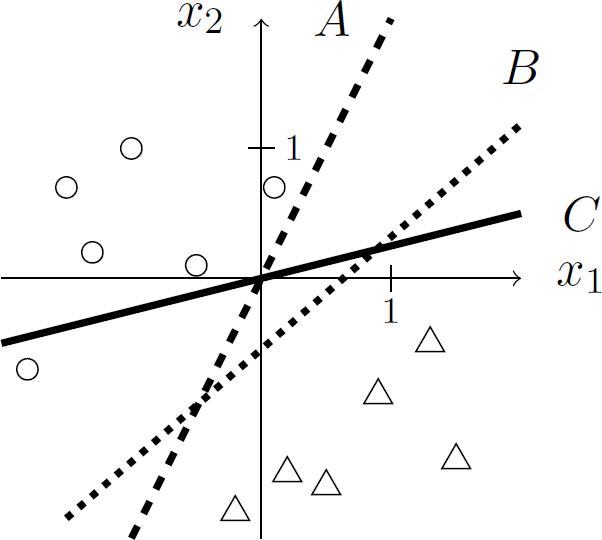
Consider the following algorithms for learning linear classifiers which could have produced the depicted classifiers given the depicted training data:
i.ThePerceptron (making one pass over the training data, e., T = n).
ii.An arbitrary but fixed algorithm that minimizes training error for homogeneous linearclas- sifiers. Machine Learning代考
iii.An algorithm that exactly solves the non-separable SVM optimization criterion. That is, SVMwith slack variables optimization criterion.
What is the most likely correspondence between these algorithms and the depicted linear classi- fiers? Explain your matching to receive credit.
(b)(12 points)
You are given a binary classification problem in R2 using features f1 and f2. For each of the following data preprocessing techniques, state and justify what happens to the training accuracy of any training error minimizing algorithm for homogeneous linear classifification.
You should choose between the following options:
A.Thepreprocessing can only improve the performance.
B.Thepreprocessing absolutely does not change performance. Machine Learning代考
C.Thepreprocessing can only worsen the performance.
D.Thepreprocessing can either improve or worsen theperformance.
i.Scalingthe feature space: that is, apply the map (f1, f2) (cf1, cf2) (for some fixed constant c > 0 that is selected independently, without considering the training data)
ii.Translating the feature space: that is, apply the map (f1, f2) ›→ (f1 + c, f2 + c) (for some fixed constant c ƒ= 0 that is selected independently, without considering the training data)
iii.Augmenting the feature space: that is, apply the map (f1, f2) ›→ (f1, f2, c) (for some fixed constant c ƒ= 0 that is selected independently, without considering the training data)
iv.z-scoringthe feature space: that is, apply the map 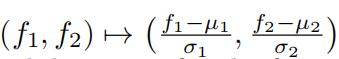
v.Combiningthe feature space: by applying the map (f1, f2) ›→ (f 2, f1f2, f 2)
vi.Combiningthe features: by applying the map (f1, f2) ›→ (f1 + f2)
5. [Nearest Neighbor Classiftcation] Machine Learning代考
(a)(5 points) Two classifiers are said to be equal if on every test example they output the same prediction.Alice, Bob and Carol each construct a 3-NN classifier using the same training dataset S. They used the following distance metrics:
dalice(x, xj) := ||x − xj||
dbob(x, xj) := 2e||x−xt ||+1
dcarol(x, xj) := ||x − xj||1
Whose classifiers would be equal for all non-empty training sets S? Justify your answer.
(b)(5 points)
Define hk(x; S) as the k-nearest neighbor classifier that takes in a training dataset S and a test example x and outputs a prediction yˆ ∈ {0, 1}. (so, h5(x, Si) denotes the 5-NN classifier that is trained on Si and predicts on x). Let S1 and S2 be two disjoint training datasets from the same underlying distribution, and consider the following statements:
A.If h1(x, S1) = 1 and h1(x, S2) = 1, then h1(x, S1∪ S2) = 1.
B. If h1(x, S1) = 1 and h1(x, S2) = 1, then h3(x, S1∪ S2) = 1. Machine Learning代考
C. If h3(x, S1) = 1 and h3(x, S2) = 1, then h3(x, S1 ∪ S2) = 1.
Which of the following statements is correct? (Justify your answer)
i.Only A. iscorrect
ii.Only B. iscorrect
iii.Only C. iscorrect
iv.Only and B. are correct
v.Only and C. are correct
vi.Only and C. are correct
vii.All B. and C. are correct
viii.Noneof the B. and C. are correct
(c)Just like the Perceptron or the SVM algorithm, you want to design a ‘Kernelized’ version of k-NearestNeighbor Since distance computations are at the core of any NN algorithm, you realize that in order to develop a successful ‘kernel’-NN algorithm, you need a way to efficiently compute distances in a (possibly infinite dimensional) Kernel space. Let Φ : Rd RD denote an explicit mapping into a kernel space (where D can possibly be infinite). Machine Learning代考
i.(5 points) Show that Euclidean distances between data points in a kernel space can be writtendown as dot products, and thus can be computed efficiently for certain kernel trans- formations. That is, show that one can write:
||Φ(x) − Φ(xj)||
just in terms of the dot products .Φ(x) · Φ(xj)Σ.
ii.(5 points) Write down the pseudo-code for Kernelized 1-Nearest Neighbor. Assume that you have access to the kernel function Kφ: (x, xj) φ(x) φ(xj) , that gives you the dot product in the feature space φ.
Kernel 1-Nearest Neighbor Algorithm
Inputs:
–Trainingdata: (x1, y1), (x2, y2), . . . , (xn, yn)
–Kernel function: Kφ(,·)
–Test point:xt
Output:
–Predictionon the test point: yˆt
Pseudo-code:
6.[Regression (10 points)] Machine Learning代考
You want to design a regressor with good prediction accuracy. Knowing thatvarious kinds of regularizations help, you decide to incorporate both the lasso and ridge penalties in the design of your optimization Given training data (x1, y1), . . . , (xn, yn) (where each xi ∈ Rd and each yi ∈ R) you come up with the following optimization
where: (i) X is a d × n data matrix where the ith column corresponds to training data xi, (ii) y is a 1 × n output vector where the ith component corresponds to the training output yi, and (iii) w is a 1 × d parameter weight vector. λ ≥ 0 and α ∈ [0, 1] are known trade-off parameters.
Show that this optimization can be turned into a lasso regression by appropriately augmenting the training data.
更多代写:C++代考推荐 托福代考 Coursework英国代写 2000essay怎么写 application letter代写 作业代写枪手
合作平台:essay代写 论文代写 写手招聘 英国留学生代写