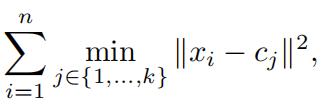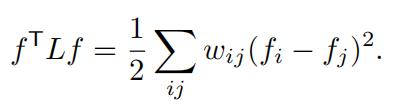COMS 4771 HW4 (Spring 2022)
Cs代做价格 Part (e) gives us some indication on why the transformation V (low order spectra of L) is a reasonable representation.
This homework is to be done alone. No late homeworks are allowed. To receive credit, a type- setted copy of the homework pdf must be uploaded to Gradescope by the due date. You must show your work to receive full credit. Discussing possible approaches for solutions for homework ques- tions is encouraged on the course discussion board and with your peers, but you must write your own individual solutions and not share your written work/code. You must cite all resources (includ- ing online material, books, articles, help taken from/given to specific individuals, etc.) you used to complete your work.
1 VC dimension
Compute the tightest possible VC dimension estimate of the following model classes:
(i)F:= {fα : x ›→ i 1[xi ≤ αi] | α = (αi)i∈{1,…,d}, αi ∈ R}, for a fixed dimension d ≥ 1.
(ii)F:= Convex polygons in R2, where the interior (and the boundary) is labelled negative and the exterior is labelled positive.
2 From distances to embeddings cs代做价格
Your friend from overseas is visiting you and asks you the geographical locations of popular US cities on a map. Not having access to a US map, you realize that you cannot provide your friend accurate information. You recall that you have access to the relative distances between nine popular US cities, given by the following distance matrix D:
| Distances (D) | BOS | NYC | DC | MIA | CHI | SEA | SF | LA | DEN |
| BOS | 0 | 206 | 429 | 1504 | 963 | 2976 | 3095 | 2979 | 1949 |
| NYC | 206 | 0 | 233 | 1308 | 802 | 2815 | 2934 | 2786 | 1771 |
| DC | 429 | 233 | 0 | 1075 | 671 | 2684 | 2799 | 2631 | 1616 |
| MIA | 1504 | 1308 | 1075 | 0 | 1329 | 3273 | 3053 | 2687 | 2037 |
| CHI | 963 | 802 | 671 | 1329 | 0 | 2013 | 2142 | 2054 | 996 |
| SEA | 2976 | 2815 | 2684 | 3273 | 2013 | 0 | 808 | 1131 | 1307 |
| SF | 3095 | 2934 | 2799 | 3053 | 2142 | 808 | 0 | 379 | 1235 |
| LA | 2979 | 2786 | 2631 | 2687 | 2054 | 1131 | 379 | 0 | 1059 |
| DEN | 1949 | 1771 | 1616 | 2037 | 996 | 1307 | 1235 | 1059 | 0 |
Being a machine learning student, you believe that it may be possible to infer the locations of these cities from the distance data. To find an embedding of these nine cities on a two dimensional map, you decide to solve it as an optimization problem as follows. cs代做价格
You associate a two-dimensional variable xi as the unknown latitude and the longitude value for each of the nine cities (that is, x1 is the lat/lon value for BOS, x2 is the lat/lon value for NYC, etc.). You write down the an (unconstrained) optimization problem
where  denotes the embedding discrepancy function.
denotes the embedding discrepancy function.
(i)What is the derivative of the discrepancy function with respect to a locationxi?
(ii)Writea program in your preferred language to find an optimal setting of locations x1, . . . , x9. You must submit your code to receive full
(iii)Plot the result of the optimization showing the estimated locations of the nine cities. (here is a sample code to plot the city locations inMatlab)
>> cities= ’BOS’,’NYC’,’DC’,’MIA’,’CHI’,’SEA’,’SF’,’LA’,’DEN’ ;
>> locs = [x1;x2;x3;x4;x5;x6;x7;x8;x9];
>> figure; text(locs(:,1), locs(:,2), cities);
What can you say about your result of the estimated locations compared to the actual geo- graphical locations of these cities?

3 Studying k-means cs代做价格
Recall that in k-means clustering we attempt to find k cluster centers cj Rd, j 1, . . . , k such that the total (squared) distance between each datapoint and the nearest cluster center is minimized. In other words, we attempt to find c1, . . . , ck that minimizes
where n is the total number of datapoints. To do so, we iterate between assigning xi to the nearest cluster center and updating each cluster center cj to the average of all points assigned to the jth cluster (aka Lloyd’s method).
(i)[it is unclear how to find the best k, e. estimate the correct number of clusters!]Instead of holding the number of clusters k fixed, one can think of minimizing (1) over both k and c. Show that this is a bad idea. Specifically, what is the minimum possible value of (1)? what values of k and c result in this value?
(ii)[suboptimality of Lloyd’s method] For the case d = 1 (and k 2), show that Lloyd’s algorithm is not That is, there is a suboptimal setting of cluster assignment forsome dataset (with d = 1) for which Lloyd’s algorithm will not be able to improve the solution. cs代做价格
(iii)[improving k-means quality] k-means with Euclidean distance metric assumes that each pair of clusters is linearly separable (see part ii below). This may not be the desired result. A classicexample is where we have two clusters corresponding to data points on two concentric circles in the R2.
(a)ImplementLloyd’s method for k-means algorithm and show the resulting cluster assign- ment for the dataset depicted above. Give two more examples of datasets in R2, for which optimal k-means setting results in an undesirable clustering. Show the resulting cluster assignment for the two additional example
(b)Show that for k = 2, for any (distinct) placement of centers c1and c2 in Rd, the cluster boundary induced by minimizing the k-means objective (i.e. 1) is necessarily linear.
One way to get a more flexible clustering is to run k-means in a transformed space. The transformation and clustering is done as follows:
- Letttr denote the r-nearest neighbor graph induced on the given dataset (say the dataset has n datapoints), that is, the datapoints are the vertices (notation: vi is the vertex associ- ated with datapoint xi) and there is an edge between vertex vi and vj if the corresponding datapoint xj is one of the r closest neighbors of datapoint xi.
- Let W denote the n ×n edge matrix, where
wij = 1[∃ edge between vi and vj in ttr].
- Definen × n diagonal matrix D as dii := j wij, and finally define L = D − W .
- Compute the bottom k eigenvectors/values of L (that is, eigenvectors corresponding to the k smallest eigenvalues). Let V be the n k matrix of of the bottom eigenvectors. One can view this matrix V as a k dimensional representation of the n datapoints.
- Run k-means on the datamatrix V and return the clustering induced.
We’ll try to gain a better understanding of this transformation V (which is basically the lower order spectra of L).
(c)Show that for any vector f ∈Rn,
- L is a symmetric positive semi-definite
- Letthe graph ttr have k connected components C1, . . . , Ck. Show that the n 1 indica- tor vectors 1Ck , . . . , 1Ck are (unnormalized) eigenvectors of L with eigenvalue 0. (theith component of an indicator vector takes value one iff the vertex vi is in the connected component) cs代做价格
Part (e) gives us some indication on why the transformation V (low order spectra of L) is a reasonable representation. Basically: (i) vertices belonging to the same connected componen- t/cluster (ie, datapoints connected with a “path”, even if they are located far away or form odd shapes) will have the same value in the representation V = [1C1 , . . . , 1Ck ], and (ii) vertices belonging to different connected component/cluster will have distinct representation. Thus making it easier for a k-means type algorithm to recover the clusterings.
(f)Foreach of the datasets in part (i) (there are total three datasets), run this flexible version of k-means in the transformed space. Show the resulting clustering assignment on all the Does it improve the clustering quality? How does the choice of r (in ttr) affects the result?
(You must submit your code for parts (a) and (f) to receive full credit. All plots and analysis must be included in the pdf document.)
更多代写:CS代码编程代做 gmat线上考试作弊 PSY心理学网课代上 Psychology Essay代写 Proposal论文代写 Argument essay怎么写
合作平台:essay代写 论文代写 写手招聘 英国留学生代写

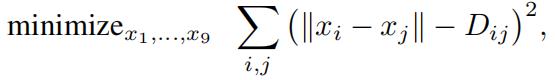
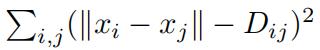 denotes the embedding discrepancy function.
denotes the embedding discrepancy function.