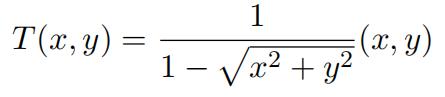Final
Calculus期末代考 Let S be the surface defined in cylindrical coordinates by r = 1 + z2, r 3, oriented with normals pointing towards the z-axis.
1.(20Points, Parts abc) Flux wave
Let K be the cylindrical surface (x — z)2 + (y — z)2 = 1 in R3. Let S be the portion of the surface z = sin x cos y inside the region (x — z)2 + (y — z)2 1. Let
(x, y, z) = (1 + x — y)(1, 1, 1).
a.Find a continuous unit normal vector field onK.
b.Sketch K and your chosen normalfield on the same diagram.
c.Calculate the flux of
through S oriented with normals pointing upwards.
2.(20Points, Parts ab) Double integral Calculus期末代考
Let D denote the unit disk in R2given by: x2 + y2 < 1.
a.Consider the map R2 defined by:
Show that T is a di↵eomorphism, that is, T is C1, injective (1-1), surjective (onto), and has C1 inverse.
b.Compute
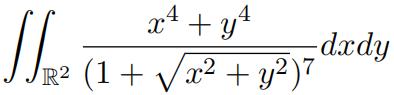

3.(20Points, Parts ab) Loops and flux
a.Recall that (You may assume this without proof.)
Consider the vector field
(i)What is the (maximal) domain D of ? Is
conservative on D?
(ii)Is conservative on the upper half-plane {(x, y) 2 R2|y > 0} ?
(iii)LetCa,b be the circle in R2 of radius 2, centered at (a, b), traversed
Consider (a, b) such that Ca,b lies in the domain D of . Determine the maximum value of
and describe all (a, b) which achieve this value.
b.Let Calculus期末代考
Let S be the surface defined in cylindrical coordinates by r = 1 + z2, r 3, oriented with normals pointing towards the z-axis. Divide S into the portion S+ lying above the xy-plane, and the portion S— lying below the xy-plane.
Determine whether the flux of F~ through S+ or S— is larger.
4.(20 Points) Surfaceintegral
Let S be the portion of the surface x4 + y4 + z4 = 1 lying in the first octant in R3 (i.e. x ≤ 0,y ≤ 0,z ≤ 0),oriented with normals pointing away from the origin. Calculate where
(x, y, z) = (x2yz + sin(yz), xy2z + sin(xz), xyz2 + sin(xy)).
5.(Parts abc)AMGM Calculus期末代考
(a)(4Points) Consider the map Φ(xi, · · , xn) = (y1, ·· · , yn) defined by (where this expression makes sense).
(i)Is the (maximal) domain of Φ closed and bounded? (You do not need to provide a proof.)
(ii)Isthe image of Ø closed and bounded? (You do not need to provide a proof.)
(b)(10Points) Using calculus techniques, prove that x2x2 · · for any x , ·· · ,x .
(c)(6 Points) Deduce the arithmetic mean – geometric mean inequality, that is, if a1, · · , an> 0,then
6.(20 Points, Parts abcde)True/False Calculus期末代考
Circle whether or not the corresponding statement is TRUE or FALSE. Briefly justify your answer with a proof or counterexample. Important: Points will be awarded as follows:
(4 points) for correct answer with justification;
(3 points) for correct answer with promising but incomplete justification; (2 points) for correct answer;
(1 point) for no answer;
(0 points) for incorrect answer. Calculus期末代考
a.If is a nonconstant flow line of a C2 vector field
decreasing function of t.
TRUE/FALSE
b.LetD = R3 \ {x = z = 0} denote 3D space with the y-axis removed.If is a C2 vector field defined on D and curl ≡ 0, then
for some real valued function f on D.
TRUE/FALSE
c.Let f : R2 → R be a C2 function such that and detH(f )(0, 0) ≤ 0, where H(f ) is the Hessian (matrix of second partial derivatives).Then f has a local minimum at (0,0).
TRUE/FALSE
d.Usinglinear approximation of the function f (x, y, z) = ex+2yx+3y+z3 at (0, 0, 0), we can esti- mate f (0.01, 0.01, 0.03) by 1.
TRUE/FALSE
e.Define f :
Then lim(x,y)→(0,0)f (x, y) = 0.
TRUE/FALSE
更多代写:金融代上网课 gre?proctoru代考 加拿大留学代写 加拿大毕业论文代写 会计英文论文作业代写 如何写好论文
合作平台:essay代写 论文代写 写手招聘 英国留学生代写