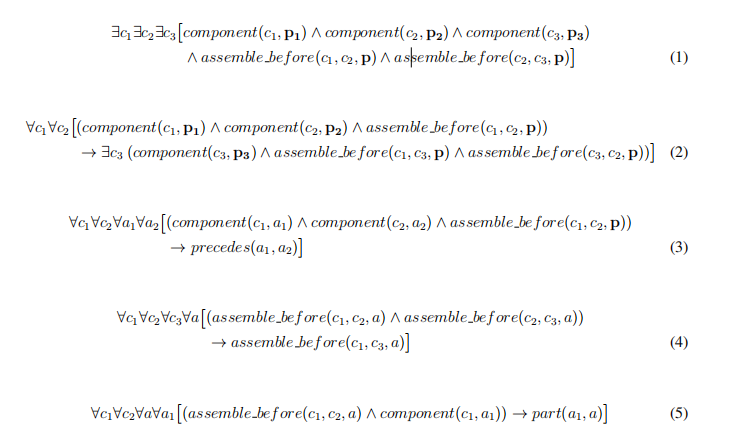Bayes代写 - 贝叶斯代写 - Take Home代写

Computer Science 384

Take Home Exam: Bayes Nets and Knowledge Representation

Bayes代写 Silent Policy: A silent policy will take effect 24 hours before this assignment is due, i.e. no questions will be answered, whether asked on···

Silent Policy:

A silent policy will take effect 24 hours before this assignment is due, i.e. no questions will be answered, whether asked on the discussion board, via email or in person.

Policies: Bayes代写

TheTAs and instructors will continue to hold office hours and host help sessions between April 3rd and the due date. However, during these sessions, you may not discuss problems on the take home exam. Instead, you can discuss practice problems that have been posted to the website. Similarly, on Piazza, you may not discuss problems on the take home You can instead discuss practice problems.
You must work alone on this take home exam.You may not discuss problems on the take home exam with anyone (including other students).
Youmust write your answers clearly and legibly for full
Nosubmissions will be accepted past the due date without approval.
Therewill be no auto-fail policy associated with this

Total Marks: This exam represents 20% of the course grade.

Handing in this Assignment Bayes代写

What to hand in electronically: Submit written answers in a file called answers.pdf as well as acknowledgment form.pdf using MarkUs. Your login to MarkUs is your teach.cs username and pass- word. It is your responsibility to include all necessary files in your submission.

Clarification Page: Important corrections (hopefully few or none) and clarifications to the assignment will be posted on the Exam Clarification page, linked from the CSC384 web page, also found at: http:

//www.teach.cs.toronto.edu/~csc384h/winter/tests.html. You are responsible for monitoring the Exam Clarification page.

Questions: Questions about the exam should be asked on Piazza:

https://piazza.com/utoronto.ca/winter2020/csc384/home.

You may also reach out to the TAs or one of the instructors. Please place ”Exam” and ”CSC384” in the subject line of your email.

Q1. Probability (worth 15/100 marks) Bayes代写

(worth 2 marks) There is a type of skin cancer that affects 3 in every 100 people.A company has invented a test that can diagnose this cancer using an The test isn’t perfect, tho; it will give a false positive (i.e. it will detect cancer when there is none) 5% of the time and a false negative (i.e. it will fail to detect a cancer that is present) 3% of the time.

If a test is positive, what is the probability the patient does not have cancer? If a test is negative, what is the probability the patient does have cancer?

(worth3 marks) Doctors are not happy with the false positive rate of the The company responds by creating a new test that has a false positive rate of 6% and false negative rate of 4%. Although the test seems worse than the original, the company explains the test results are conditionally indepen- dent of one another given the condition of the user. They suggest using both tests in conjunction to improve the false positive rate. Specifically, they suggest doctors diagnose cancer if and only if both tests are positive. Does this logic make sense? Explain.
(worth 5 marks) We briefly discussed what it might mean to create an ’unbiased’ Bayesian Clas- sifier.Specifically, we said that if C is a classification, Y is a label representing ’ground truth’ and A is some ’protected attribute’ (e.g. gender or race) we might enforce Separation of classifications, making A independent of C given Y . Alternately we might enforce Sufficiency, making A is in- dependent of Y given C. But we can’t do both at the same time! Show that this is true, i.e. that enforcing both Separation and Sufficiency implies A is independent of (Y, C).
(worth5 marks) Given that X is independent of Y given Z and X is independent of W given (Y, Z). Show that X is independent of (Y, W ) given Z.

Q2. Variable Elimination (worth 13/100 marks) Bayes代写

Birds frequently appear in the tree outside of your window in the morning and evening; these include finches, cardinals and robins. Finches appear more frequently than robins, and robins appear more fre- quently than cardinals (the ratio is 7:4:1). The finches will sing a song when they appear 7 out of every 10 times in the morning, but never in the evening. The cardinals rarely sing songs and only in the evenings (in the evening, they sing 1 of every 10 times they appear). Robins sing once every five times they appear regardless of the time of day. Every tenth cardinal and robin will stay in the tree longer than five minutes. Every fourth finch will stay in the tree longer than five minutes.

(worth2 marks) Draw a Bayesian network that captures the information in the story above correctly and concisely. Make sure to annotate your network with conditional probability tables (CPTs).
(worth 1 mark) How many parameters will be required to specify the network you have drawn?
(worth 5 marks) A bird lands in the tree in the morning.What is the probability that it will stay in the tree longer than five minutes?
(worth5 marks) What is the overall probability that any given bird in your tree will sing a song?

Q3. Markov Models (worth 12/100 marks) Bayes代写

In the mail room of a university office, a stream of blue and yellow mail carts pass a mail sorting robot. Blue carts contain 7 domestic letters for every 3 international letters. Yellow carts contain 2 domestic letters for every 3 international letters. Blue carts are followed by blue carts 70% of the time, but 30% of the time they are followed by a yellow cart. Yellow carts are followed by yellow carts half of of the time, and the other half of the time they are followed by a blue cart. The first cart, every morning, is yellow 9 of every 10 times.

The robot pulls a single letter from each cart as the cart passes it by.

(worth 2 mark) Draw a markov model to represent the joint distribution over cart colors and the origins of letters selected by the robot.Include a conditional probability table (CPT) with each variable in your model.
(worth 5 marks) What is the probability that the first three letters selected by the robot, in order, will be:domestic, international, domestic?
(worth 5 marks) What is the probability that the fourth cart will be blue if the first three letters selected, in order, are: international,international, domestic?

Q4. D-Separation and Relevance (worth 10/100 marks) Bayes代写

Given the Bayesian Network structure above ….

(worth1 mark) How many parameters are required to fully specify the network?
(worth3 marks) List three pairs of variables X, Y where X is independent of Y .
(worth3 marks) List three sets of variables X, Y, Z where X is independent of Z given Y .
(worth1 mark) Assume we are to calculate P (B|E, F ). Which variables are relevant?
(worth2 marks) Assume we are to calculate P (B G) using variable elimination. List the elimina- tion order you might suggest when using the min-fill heuristic to select variables, and give the size of the factors that result from each elimination.

Q5. First-order Structures and Models (worth 19/100 marks) Bayes代写

Consider a first-order language _metal consisting of constant symbols o₁, o₂, o₃, a binary predicate symbol

heavier than, and unary predicate symbol expensive. Let D = {Steel, Aluminium, Titanium}.

Q6. Proof by Resolution (worth 31/100 marks)

Consider the following knowledge base (note that p, p₁, p₂, p₃ are constant symbols, part(x, y) means x is a part of y and precedes(x, y) means x precedes y):

(worth11 marks) Convert the sentences to clausal form.
(worth20 marks) Use resolution to answer the following

You must use the notation developed in class (see slide no 39 in KRR-Part 2) for presenting your answers.

(worth10 marks) What is a part of p? (finding one answer is sufficient) Note: part(x, y) denotes x is a part of y.
(worth10 marks) What does precede p₃? (finding one answer is sufficient) Note: precedes(x, y) denotes x precedes y.

合作平台：天才代写幽灵代写写手招聘 paper代写