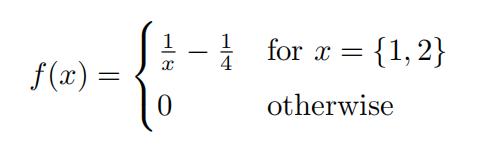Sample Final
数据分析统计final代写 Does using a one-tailed test makes it harder to reject the null hypothesis? Does it change theprobability of making a type I error?
1.True/FalseIf you know the relevant CDF, you can fully describe the random variable.
2.True/FalseThe shortcomings of a convenience sample can be offset with weighting techniques.
3.True/False The population mean, µ, is a random variable.
4.True/False A problem with the randomization protocol and non-compliance in an experiment are issues of external variable.
5.Does using a one-tailed test makes it harder to reject the null hypothesis? Does it change the probability of making a type I error?
6.Isthe function below a valid PMF, PDF, CDF, or none of those things?
It is a valid PMF! The function is always non-negative: f (x) 0 for all x. Also, the sum of the probabilities equals 1: Σall x f (x) = ( 1 − 1 ) + ( 1 − 1 ) = 3 + 1 = 1.
7.Arecycling bin contains 6 coke cans, 2 diet coke cans, 5 coke bottles, and 5 diet coke bottles. 数据分析统计final代写
(a)What is the probability of pulling a diet coke container from thebin?
(b)Whatis the probability of pulling a diet coke container from the bin given that it is a can?
(c)Whatis the probability of pulling a can conditional on having drawn a single bottle (without replacement)?
(d)What is the probability of pulling a can conditional on having drawn a single bottle (with replacement)?
(e)Suppose that cans are worth $0.05 for their deposit and that bottles are worth $0.10 for their deposit. What is the expected value in deposits from pulling a single soda container from the bin?
8.Suppose a town has four quadrants: NE, NW, SE, and SW.
The expected level of water contam- ination for households is 8 parts per million (ppm) for households in the NE quadrant, 6 ppm for households in the NW quadrant, 12 ppm for households in the SE quadrant, and 16 ppm for householdsin the SW Within the town, 1,500 households live in the NE quadrant, 1,000 live in the NW quadrant, 500 live in the SE quadrant, and 2,000 live in the SW quadrant. What is the expected level of water contamination for a household in the town? 数据分析统计final代写
9.Bala, Baka, and Bama are preparing for final exams. They want to attend the professor’s office hours that are the least crowded. Bama is in Professor Moskowitz’s class and can never get out of the wait room for his afternoon office hours. Baka is in Professor Frank’s class but his office hours are canceled due to an internet outage.
Bala is in Professor Lo’s class and claims that his office hours are also always packed. Baka proposes a hypothesis test to determine if the mean attendance at Professor Lo’s and Professor Moskowitz’s office hours are different. What information do Baka andBala need to test this hypothesis? Which formula should they use to calculate the test statistic?

10.Supposeyou’re a member of the city council and you’re in charge of studying use of local roads by small and large capacity truckers. 数据分析统计final代写
You are interested in the load size of trucks that use the primary roads in your town. There are 200 small-capacity trucks and 70 large-capacity trucks that use your town’s roads on a regular basis. You decide to stratify the sample. You sample 74 small-capacity trucks and 56 large-capacity trucks. Calculate the sampling weight, wL, you would use for the large-capacity trucks for your stratified sample, and calculate the weight, wS, you would use for the small-capacity trucks?
11.Suppose,from a random sample of 1,040 residents of Chicago, 22% of residents had antibodies for Covid-19. Calculate a 95% confidence interval for this estimate and provide a correct interpretation of it. Then calculate a 90% confidence interval.
12.ConsiderBriar and Billie’s estimators for the population mean:
Determine whether each estimator is unbiased and consistent.
13.A researcher is interested in whether eating breakfast is associated with better performance on tests. She collected the data below and asked for your help analyzing it. Specifically, she wantsto conduct a formal test as to whether the mean test score for breakfast-eaters is greater than the mean test score for breakfast-non-eaters.
(a)Which of the following is the most appropriate hypothesis test touse?
i.Chi-squared test
ii.Fisher’s exact test
iii.Two-samplez-test
iv.Two-samplet-test
v.One-samplez-test
vi.One-samplet-test
vii.Two-samplez-test
viii.Pairedt-test
ix.Welch’s two-sample t-test for unequalvariances 数据分析统计final代写
x.Exact binomial test
(b)What are the null and alternativehypotheses?
(c)Does the alternative hypothesis imply a one-sided test, two-sided test, or are both equally appropriate?
(d)Usingthe hypothesis test you indicated in the question above, calculate the test statistic.
Round it to two decimal places.
(e)Do you reject or fail to reject the null hypothesis at the α = 0.05 significancelevel?
14.Consider the results from a descriptive regression examining the relationship between absenteeism rates, party affiliation, and “ruralness” in a recent session of a state legislature.
The absenteeism rate (absenteeism) indicates the proportion of roll-call votes that a legislator missed, so the variable= 0 for a legislator with perfect attendance, = 1 for a legislator who missed 100% of votes, and= 0.10 for a legislator who missed 10% of votes. The legislature only contains Democrats and Republicans, and the variable democrat is coded = 1 if the legislator is a Democrat and = 0 otherwise.
Finally, the variable rural indicates the proportion of the district’s population residing in a rural area. For instance, rural is coded = 1 for a legislative district comprised entirely of rural residents, = 0 for a district comprised entirely of non-rural residents, and = 0.10 for a district comprised of 10% rural residents and 90% non-rural residents. Several legislators from both parties in the sample represent entirely rural and entirely non-rural districts. Make sure to indicate the appropriate units.
my.reg <- lm(absentee ~ democrat + rural, data = state.leg) coef(my.reg) ## (Intercept) democrat rural ## .30 -0.05 0.10
(a)Calculate predicted values for thefollowing:
i.A Republican representing a 100% rural district.
ii.A Republican representing a 10% rural district.
iii.A Democrat representing a 90% ruraldistrict:
iv.A Democrat representing a 0% ruraldistrict:
(b)Provide a correct interpretation of both estimated coeffiffifficients. 数据分析统计final代写
(c)Provide a correct interpretation of the estimated intercept. Do we know if the intercept is substantively meaningful in this context?
(d)Can this regression tell us whether the relationship between rural and absentee varies byparty affiliation? If not, indicate a single regression that would allow us to determine if the relationship varies by party.
15.Suppose we are interested in the effect of a high-quality mask on Covid infection risk.We recruit a group of 1,000 individuals for our We randomly assign 500 to receive a weekly supply of N95 masks, and we randomly assign 500 to a control group that doesn’t receive free masks. At the conclusion of the study, our data indicate that 25 members of the N95 group had contracted Covid, and 50 members of the control group had contracted Covid.
Suppose we further learn that, of those randomly assigned to the N95 group, 250 refused to wear an N95 (they claimed it was too uncomfortable). No one in the control wore an N95 mask during the period under study. Estimate the following quantities (if they are possible to estimate): the intent-to-treat effect and the complier average treatment effect.
更多代写:python代寫 托福代考 英国POL政治代写 英文Essay代写 英文科技论文代写 商科网课代修