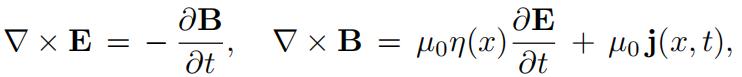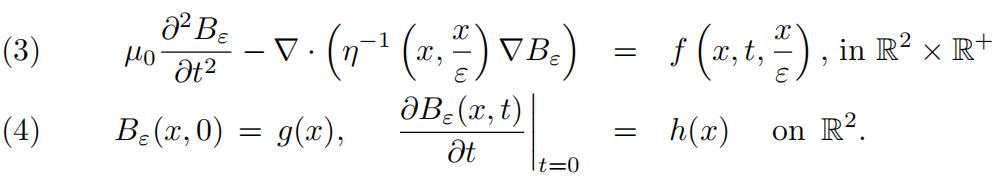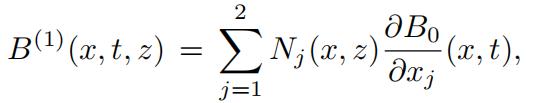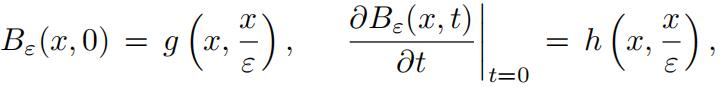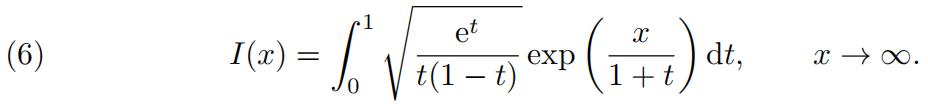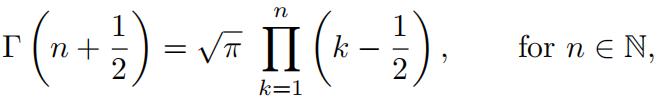数学建模代考-MATH0087代写-Mathematical modeling代写

MATH0087

数学建模代考 where positive smooth function η(x) is electric permittivity and positive constant µ0 is magnetic permeability of the medium.

Answer all questions.

1. 数学建模代考

Considerthe following model of a transverse magnetic electromagnetic field in an inhomogeneous two-dimensional electromagnetic medium occupying domain Ω due to distributed current source j(x, t) = (j₁(x, t), j₂(x, t), 0) in the in-plane direction, where x = (x₁, x₂) and t Magnetic field B is assumed to be orthogonal to the plane, i.e. B = B(x)k where k is the unit vector in the positive x₃-direction. The magnetic field B is related to the electric field E(x) via Maxwell’s equations as follows

∂B ∂E

(1)

where positive smooth function η(x) is electric permittivity and positive constant µ₀ is magnetic permeability of the medium.

(a)Showthat B(x, t) is a solution of an inhomogeneous wave equation

(5 marks)

(b)Let the exterior boundary S of Ω be perfectly conducting, i.e. E× n = 0 on S where n is the outward unit normal to S. Let for the initial magnetic field at t = 0, B(x, 0) = B₀(x), x ∈ Ω, and the initial electric field E at t = 0 be E₀(x) = (E₀₁(x), E₀₁(x), 0). Derive the resulting initial boundary-value problem for B.(5 marks)

(c)Showthat the initial boundary-value problem of part (c) has no more than one solution.(10 marks)

2.Consider the following initial-value problem describing propagation of transverse- magnetic electromagnetic waves in an unbounded two-dimensional two-scale het- erogeneousmedium: 数学建模代考

Here x = (x₁, x₂) R2, the smooth functions η(x, z) > 0 and f (x, t, z), z = (z₁, z₂) R2, describing microscopic electric permittivity and sources due to cur- rents respectively, are both periodic in z with periodicity cell Q = [0, 1]²; constant µ₀ > 0 is magnetic permeability of the medium. The smooth functions η(x, z), f (x, t, z), g(x) and h(x) are independent of ε, where ε > 0 is a small parameter.

You are given that the solution B_ε(x, t) to (3)–(4) has an asymptotic approxi-mation in the two-scale form:

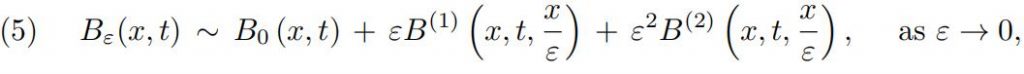
where B⁽¹⁾(x, t, z) and B⁽²⁾(x, t, z) are periodic in z with the periodicity cell Q.

(a)Byequating the terms of the order ε⁻¹ in (3) show that

where N_j(x, z), j = 1, 2, are independent of B₀. Show that N_j(x, z) are the solutions to the “unit cell” problems, and formulate those problems.(5 marks)

(b)Byequating the terms of the order ε⁰ in (3), derive the equation for B₀ (the homogenised equation). Find the components η^h (x) of the homogenised electric permeability matrix η^h(x), and the homogenised source f ^h(x, t) in terms of η(x, z), µ₀, f (x, t, z) and N_j(x, z), j = 1, 2.(8 marks)

(c)Formulate the homogenised initial-value problem (but do not attempt to solveit).(2 marks)

(d)Whatwould be the problem with the above approach if the initial conditions were also two-scale,i. e.

where g(x, z) and h(x, z) are periodic in z? Can there be any way for fixing it?(5 marks)

3.(a)Derive the first two terms in an asymptotic expansion of 数学建模代考

(5 marks)

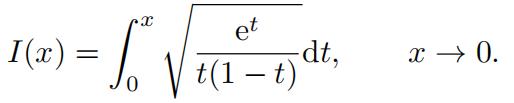
(b)Apply Laplace’s Method from first principles to derive the leadingor- der term in the asymptotic expansion of

You may re-use some of your answer to part (a) and standard identities involving the Gamma function without proof.(12 marks)

(c)Briefly explain why Integration by Parts should not be used when de- riving an asymptotic expansion of(6).(3 marks)

4.(a) Use Integration by Parts and Induction to prove thefollowing: 数学建模代考

where Γ denotes the Gamma function. You may use the identity Γ(1/2) = without proof.(6 marks)

(b)Use The Method of Steepest Descent to obtain a full asymptotic expansionof

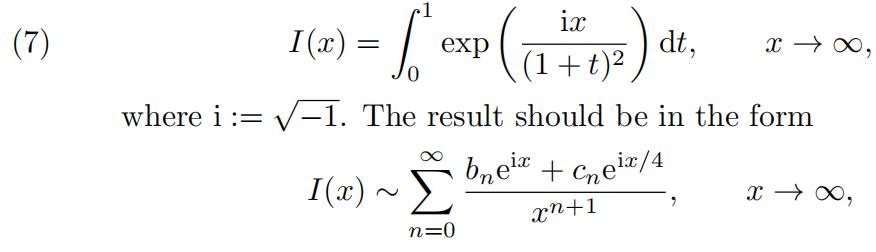
clearly defining b_n and c_n for n N. You may use Watson’s Lemma and the following identity without proof:

(c)Using an alternative method from the course notes, derive the leading order term in the asymptotic expansion of (7). You may quote general results from the notes without proof, but symbolic software solutions will not be accepted.(5 marks)

5.(a) A power-law fluid has shear viscosity η = k |γ˙| ⁿ⁻¹, where γ˙ is the shear rate, with k > 0 and n > 0.

(i)The fluid is pumped along a straight channel of depth 2H and stress- freeside walls (so that there is no velocity variation in that direction), under a pressure gradient tt. Find the velocity profiles in the channel, and sketch them qualitatively for n < 1, n = 1 and n >1. (6 marks)

(ii)The power-law fluid is ‘matched’ with a Newtonian (n = 1) fluid in the sense that under gravity they flow out of a channel held vertically upright in the same time. Suppose the channel is now tilted so as to make an angle θ with the vertical. What is the ratio of the fluxes of the power-law and Newtonianfluids?(7 marks)

(b) The Oldroyd B model has shear stress 数学建模代考

where η_s and η_p are the solvent and polymer viscosities, respectively, λ

is a relaxation time and γ˙ is the usual rate of strain. It is observed that

the solvent and polymeric viscosities for a particular Oldroyd B fluid are identical, so η_s = η_p. An experimentalist is able to apply a simple fixed shear rate γ˙ to the fluid and measure both the shear stress response τ and the normal stress difference N₁. Show that