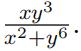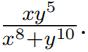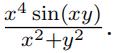博客

Exam 2 (MTH 252)-Spring 2023

微积分考试代写 Below are some problems to practice for the exam. We will discuss some of these problems during the review session.

Exam 2 will be on March 15 and covers Sections 14.1-14.7 , 15.1 and 15.2. You should review your class notes and examples discussed during our meetings. I will hold a review session for the exam on Tuesday (Mar. 14) from 4:00-5:30 pm on BAC 245. Below are some problems to practice for the exam. We will discuss some of these problems during the review session.

1.Find and sketch the domain of the following functions:  微积分考试代写

(a) f(x, y) =

(b) f(x, y) =

2.Sketch the graph of the following functions:

(a) f(x, y) = 1 − y².

(b) f(x, y) = x² + (y − 2)².

(c) f(x, y) = sin x.

3.Sketch the level curves of the following functions for k = 0, ±1; if the level curves do not exist for some of these values explain your reasoning:

(a) f(x, y) =

(b) f(x, y) = e^x + y.

(c) f(x, y) = ye^x

4.Find the limit if it exists or show that it does not exist:  微积分考试代写

(a) lim(x,y)→(0,0)(x² + y² ) ln(x² + y² ).

(b) lim(x,y)→(0,0)

(c) lim(x,y)→(0,0)

(d) lim(x,y)→(0,0)

5.Find the fifirst partial derivatives of the following functions:  微积分考试代写

(a) f(x, y) = y sec(x² + y² ).

(b) f(x, y) =

(c) p(u, v, w) = u arctan

6.Determine the set of points at which the function

is continuous.

7.If z = sin(x + sin t) show that

z_xz_xt = z_tz_xx.

8.For each equation, fifind dy/dx (assume that y is a function of x):

(a) arctan(x²y) = x + xy² .

(b) cos(xy) = 1 + sin y.

9.For the following equation, fifind ∂z/∂x and ∂z/∂x (assume that z is a function of x and y):

sin(xyz) = x² y² z² .

10.If z = y + f(x² − y² ), show that

yz_x + xz_y = x.

11.Find the equations of the tangent plane and normal line to the following surfaces at the given point:

(a) xy + yz + zx = 3 at (1, 1, 1).

(b) z = 3x² − y² + 2x at (1, −2, 1).

12.Find the points on

x² + 4y² − z² = 4

where the tangent plane is parallel to the plane 2x + 2y + z = 5.

13.Explain why the following functions are difffferentiable at the given point. Then fifind the linear approximation of the function at that point:  微积分考试代写

(a) f(x, y) = x²e^y at (1, 0).

(b) f(x, y) = y + sin(x/y) at (0, 3).

14.Find the directional derivative of each function at the point P in the given direction :

(a) f(x, y) = x 2 e y at P(1, 0) and  =

(b) f(x, y, z) = xy − xy2 z 2 at (2, −1, 1) and  =

15.Find the maximum and minimum rates of change of f at the given point and the direction in which they occur:

(a) f(x, y) = sin(xy) at P(1, 0).

(b) f(x, y, z) = x ln(yz) at (1, 2, 1).

更多代写：Management 管理学  网考怎么作弊  fin代考价格  Nursing Essay代写润色  paper统计学代写  dissertation代寫

合作平台：essay代写 论文代写 写手招聘 英国留学生代写