ECON2070
Review Tutorial
博弈论作业代写 Three (3) fifirms use water from a lake. Each fifirm has two (2) possible actions: treat sewage (T) or dump sewage (D).
Short Questions 博弈论作业代写
SQ1. Can a weakly dominated strategy be a best response? Brieflfly explain.
SQ2. Assume the stock market is low with probability 0.4 and high with probability 0.6. A lottery yields $1 if the market is low. If the market is high, the lottery yields $0 with probability 0.5 and $10 with probability 0.5. If the agent’s preferences satisfy the assumptions of the expected utility theorem, then will she choose the lottery or an offffer which gives $3 with probability 1?

Problem Solving 博弈论作业代写
LQ1. Three (3) fifirms use water from a lake. Each fifirm has two (2) possible actions: treat sewage (T) or dump sewage (D). If no or only one (1) fifirm dumps sewage, the lake remains clean. If two (2) or more fifirms dump sewage, the lake becomes polluted. Each fifirm gets a revenue of 4 if the lake is clean, and a revenue of 1 if the lake is polluted. The cost of treating sewage is 1. There is no cost to dumping sewage. Each fifirm’s payoffff is given by its revenue minus sewage treatment cost, if any.
(a) Describe this situation as a normal form game using payoffff matrices.
(b) Is there a (strongly or weakly) dominated action for each player? If yes, which one? If no, explain why. 博弈论作业代写
(c) Find all pure strategy Nash equilibria of this game.
LQ2. (Cournot’s duopoly game with imperfect information) A single good is produced by 2 fifirms. The unit cost of fifirm 1 is c, and fifirm 2’s cost is either cH or cL < cH. Firm 2 knows its cost, and fifirm 1 believes it is cL with probability θ ∈ (0, 1) and cH with probability 1−θ. If the total output is Q then the price is P(Q) = max{α−Q, 0}. Assume 0 < cL < cH < α and 0 < c < α. Find all pure strategy Bayesian Nash equilibrium of this game.
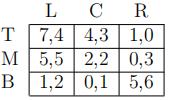
LQ3. Find all Nash equilibria (in pure and mixed strategies) of the following game.
更多代写:Statistics代写 gre助考 Python代考推荐 assignment introduction怎么写 discussion怎么写 论文essay标题
合作平台:essay代写 论文代写 写手招聘 英国留学生代写