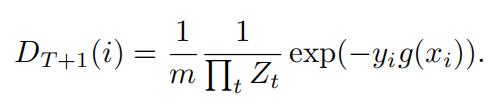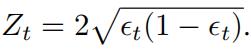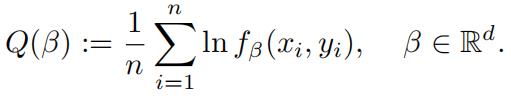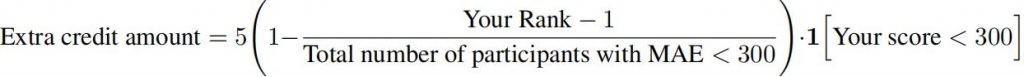博客

COMS 4771 HW3 (Spring 2022)

Due: Sun April 10, 2022 at 11:59pm

代写机器学习作业 You must cite all resources (includ- ing online material, books, articles, help taken from/given to specific individuals, etc.)

This homework is to be done alone. No late homeworks are allowed. To receive credit, a type- setted copy of the homework pdf must be uploaded to Gradescope by the due date. You must show your work to receive full credit. Discussing possible approaches for solutions for homework ques- tions is encouraged on the course discussion board and with your peers, but you must write your own individual solutions and not share your written work/code. You must cite all resources (includ- ing online material, books, articles, help taken from/given to specific individuals, etc.) you used to complete your work.

1 Combining multiple classifiers  代写机器学习作业

The concept of “wisdom-of-the-crowd” posits that collective knowledge of a group as expressed through their aggregated actions or opinions is superior to the decision of any one individual in the group. Here we will study a version of the “wisdom-of-the-crowd” for binary classifiers: how can one combine prediction outputs from multiple possibly low-quality binary classifiers to achieve an aggregate high-quality final output? Consider the following iterative procedure to combine classifier results.

Input:

-S – a set of training samples: S = (x₁, y₁), . . . , (x_m, y_m) , where each y_i1, +1

-T – number of iterations (also, number of classifiers tocombine)

-F– a set of (possibly low-quality)  Each f ∈ F, is of the form f : X → {−1, +1}

Output:

-F – a set of selected classifiers {f₁, . . . , f_T }, where each f_i ∈ F.

-A– a set of combination weights {α₁, . . . , α_T }

Iterative Combination Procedure:

-Initializedistribution weights D₁(i) = ¹ [for i = 1, . . . , m]

-fort = 1, . . . , T do

– // ϵ_j  is weighted error of j-th classifier w.r.t. D_t

-Defineϵ_j := Σm    D_t(i)  1[y_i f_j(x_i)] [for each f_j ∈ F]

– // select the classifier with the smallest (weighted) error

-f_t= arg min_fj ∈F  ϵ_j

-ϵ_t= min_fj ∈F  ϵ_j

– // recompute weights w.r.t. performance of f_t

-Computeclassifier weight α_t =  ¹ ln   ^1−ϵt

-Computedistribution weight D_t+1(i) = D_t(i) exp(−α_ty_if_t(x_i))  代写机器学习作业

-Normalizedistribution weights D_t+1(i) =  Σi Dt+1(i)

-returnweights α_t, and classifiers f_t for t = 1, . . . , T .

Final Combined Prediction:

-Forany test input x, define the aggregation function as: g(x) := t α_tf_t(x), and return the pre- diction as sign(g(x)).

We’ll prove the following statement: If for each iteration t there is some γ_t > 0 such that  ϵ_t = ¹ γ_t (that is, assuming that at each iteration the error of the classifier f_t is just γ_t better than random guessing), then error of the aggregate classifier

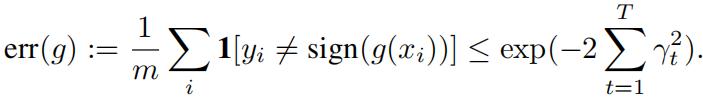
That is, the error of the aggregate classifier g decreases exponentially fast with the number of com- binations T !

(i)LetZ_t := i D_t+1(i) (i.e., Z_t denotes the normalization constant for the weighted distribu- tion D_t+1). Show that

(ii)Show that error of the aggregate classifier g is upper bounded by the product of Z_t: err(g)≤t Z_t.

(hint: use the fact that 0-1 loss is upper bounded by exponential loss)

(iii)Show that

(hint: noting , separate the expression for correctly and in- correctly classified cases and express it in terms of ϵ_t)

(iv)Bycombining results from (ii) and (iii), we have that , now show that:  代写机器学习作业

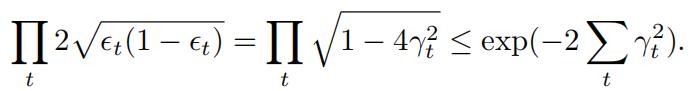
Thus establishing that

2 Estimating Model Parameters for Regression

Let P_β be the probability distribution on Rd R for the random pair (X, Y ) (where X = (X₁, . . . , X_d)) such that

X₁, . . . , X_d ∼_iid N (0, 1), and Y |X = x   ∼  N (x^Tβ, ∥x∥2),    x ∈ Rd

Here, β = (β₁, . . . , β_d) Rd are the parameters of P_β, and N (µ, σ²) denotes the Gaussian distri- bution with mean µ and variance σ².

(i)Let (x₁, y₁), . . . , (x_n, y_n) ∈ Rd × R be a given sample, andassume x_i 0 for all i =1, . . . , n. Let f_β be the probability density for P_β as defined above. Define Q : Rd → R by

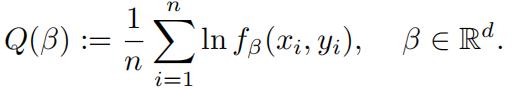
Write a convex optimization problem over the variables β  = (β₁, . . . , β_d) Rd such that its optimal solutions are maximizers of Q over all vector of Euclidean length at most one.

(ii)Let (x₁, y₁), . . . , (x_n, y_n) ∈ Rd × R be a given sample, and assume x_i̸=  0 for all i  = 1, . . . , n. Let f_β be the probability density for P_β as defined  Define Q : Rd → R by

Find a system of linear equations Aβ = b over variables β = (β₁, . . . , β_d) Rd such that the solutions are maximizers of Q over all vectors in Rd.

3 Different learning rates for different strategies (Extra Credit)  代写机器学习作业

Here will explore how the rate by which an algorithm learns a concept can change based on how labeled examples are obtained. For that we look at three settings: (i) an active learning setting where the algorithm has the luxury of specifying a data point and querying its label, (ii) a passive learning setting where labeled examples are drawn at random and (iii) an adversarial setting where training examples are given by an adversary that tries to make your life hard.

Consider a binary classification problem where each data point consists of d binary features. Let F be the hypothesis class of conjunctions of subsets of the d features and their negations. So forexample one hypothesis could be f₁(x) = x₁ ∧ x₂ ∧ ¬x_d (where ∧ denotes the logical “and” and¬ denotes the logical “not”).  Another hypothesis could be f₂(x)  =  ¬x₃ ∧ x₅.  A conjunction in F cannot contain both x_i and ¬x_i.  We assume a consistent learning scenario where there exists a hypothesis f ^∗ ∈ F that is consistent with the true label for all data points.

(i)In the active learning setting, the learning algorithm can query the label of an unlabeled ex- ample. Assume that you can query any possible example. Show that, starting with a single positiveexample, you can exactly learn the true hypothesis f ^∗ using d queries.

(ii)In the passive learning setting, where the examples are drawn i.i.d. from an underlying fixed distributionD. How many examples are sufficient to guarantee a generalization error less thanϵ with probability ≥ 1 − δ?  代写机器学习作业

(iii)Showthat if the training data is not representative of the underlying distribution, a consistent hypothesis f ^∗ can perform  Specifically, assume that the true hypothesis f ^∗ is a con- junction of k out of the d features for some k > 0 and that all possible data points are equally likely. Show that there exists a training set of 2^(d−k) unique examples and a hypothesis f that is consistent with this training set but achieves a classification error 50% when tested on all possible data points.

4 Regression Competition!  代写机器学习作业

You’ll compete with your classmates on designing a good quality regressor for a large scale dataset.

(i)Signup on http://www.kaggle.com with your columbia email address.

(ii)Visit the COMS 4771competition:

You shall develop a regressor for a large-scale dataset available there. You can use any re- source publicly available to develop your regressor. (You don’t need to submit your code for this question.)

(iio)Your pdf writeup should describe the design for your regressor: What preprocessing tech- niques and regressor you used? Why you made these choices? What resources you used and were helpful? What worked and what didn’twork?  代写机器学习作业

Make sure cite all the resources that you used.

Evaluation criterion:

• You must use your UNI as your team name in order to get points. Forexample:
  • If your uni is abc123 then your teamname should be:abc123
• Youmust get a Mean Absolute Error (MAE) score of at most 500 on the private holdout test-dataset to get full credit. (This involves employing sound ML principles in the design and selection of your best performing )
• Extra points will be awarded to the top ranked participants, using the following scoring mechanism:

 

更多代写：Network 作业辅导  GRE代考  Accountant网课代修  essay写手招聘  harvard引用格式  project代写

合作平台：essay代写 论文代写 写手招聘 英国留学生代写